1integrate this from R to 2R: (μ0I/2x)(dx/2R-R)*2
A spiral of two turns with inner radius R and outer radius 2R is placed as shown in figure. Find magnetic field at the centre of spiral.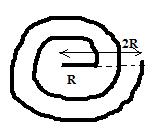
-
UP 0 DOWN 0 0 16
16 Answers
1Let inner radius be r,and outer radius be R; and no of turns be N....Now just consider a ring of radius x,
magnetic field at the centre dB=(μ0i/2x)(dx/R-r)(N)
1plz explain what kind of an element are we taking to integrate?
71I presume this sum has come in this year IIT only and also in 2009-2010 NSEP Examination.
@Subho.
You know the magnetic field at the center of a Ring. You just have to extend that idea for many spiral turns.
71The variation of radius can be neglected I think, cause we neglect many such things in physics..
Also, there should not ' 2 ' rings as shown in the figure above. It should be consisting of large closely spaced turns.
21no this is a spiral not closely placed ring.... its equation is abθ
71Spring constant is given by k = Gd4/[8nD3]
Where:
k = constant, pounds of load per inch of deflection
G = modulus of rigidity of spring material, pounds per square inch
d = wire diameter, inches
n = number of active coils, which is the number of coils subjected to flexure (always less than the total number of coils)
D = mean coil diameter, inches = Outer Diameter - Wire Diameter.
But we ignore it for our simplicity.
However, If any third party clears the doubt it will be nicer!
62The equation can be thought of as
r=kθ+l
Where θ is the angle with the positive x axis, r is the distance of the point from center and k and l are constnats.
We can find k and l because at theta = 0 , r = r
and theta = 4pi, r = 3r
Now can u try?
1@shubodip please specify the kind of spiral
you told about the nature of spiral only in #10
So,according to #10
as Told by shubodip , its a logarithmic spiral
r=R\left(2^{\frac{\theta}{4\pi}} \right)
If you notice carefully the dl element is not perpendicular to the radius vector
The figure Shows the angle formed by two curves
Had the curves exactly overlapped then we can use dl x r =dl*r
Since angle is formed ,we have dl x r = dl*r*cos(α)
where α =angle between the tangent of curves at that point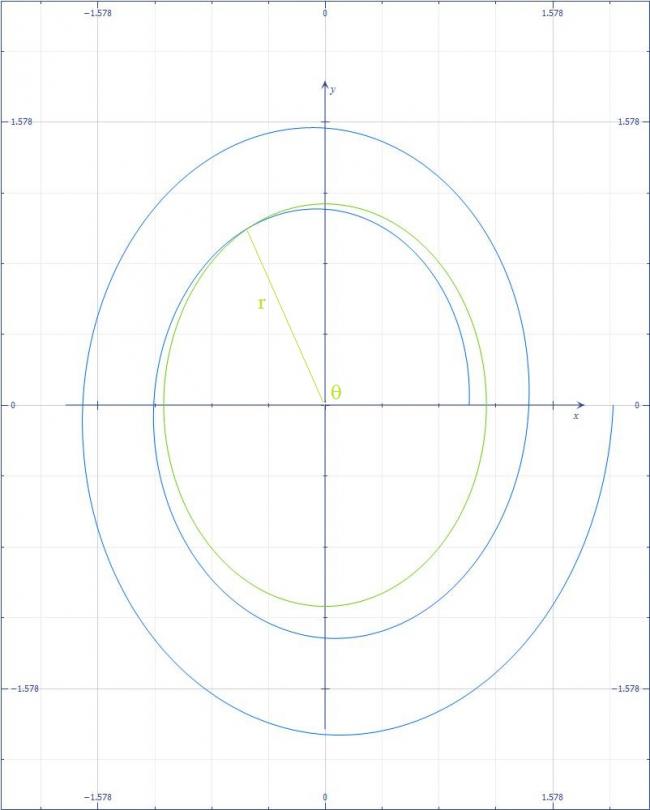
But we can make use of one thing
dl X r=r2dθ θ(cap direction)
1my attempt :
Consider the element dl as shown in figure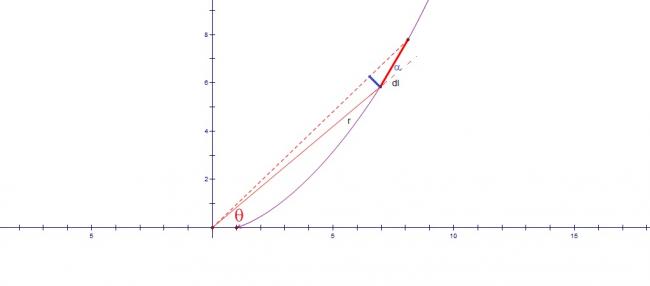
From Biot-Savart Law
\mathrm{dB=\frac{\mu_0i}{4\pi}}\left(\frac{\vec{dl} \times \hat{r}}{r^2} \right) \\ \mathrm{\vec{dl} \times \hat{r}= rd\theta \ \hat{z}}\texttt{ Consider spiral in x-y plane} \\ \mathrm{\int dB =\frac{\mu_0i}{4\pi}\int_{0}^{4\pi}\frac{d\theta}{r}} \\ \texttt{Putting r}=\mathrm{R2^{\frac{\theta}{4\pi}}} \\ \mathrm{\int dB =\frac{\mu_0i}{4\pi*R}\int_{0}^{4\pi}\frac{d\theta}{2^{\frac{\theta}{4\pi}}}} \\ \boxed{\mathrm{B=\frac{\mu_0i\ln{2}}{R}}}