1@subhodip:what is the polygon law????
1. A current loop of any arbitrary shape lies in a uniform magnetic field B. Show that the net magnetic force acting on the loop is zero.
2. Prove that the force acting on a current carrying wire, joining two fixed points a and b in a uniform magnetic field, is independent of the shape of the wire.
-
UP 0 DOWN 0 0 8
8 Answers
21F = i (dl)*(B)
wen u sum all F, it becomes i(B)Σ(dl→)
since the loop is closed Σ(dl→) = 0 (polygon law)
1for the second part simply integrate the dl vector to add up its components along ab tnus giving the displacement vector and thus the force acting on any loop is independent of the shape pf the wire.
f=i(ab)B
30@debosmit - remember the starting of vectors.. a more generalised form of traingle law .. for a polygon of n sides?
1yeah i remember....but how can u apply that to a loop of arbitrary shape????
21no..not that way...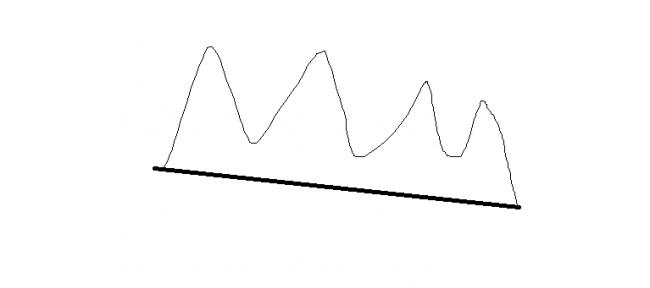
its just that join point a and b by a strght line...
since it is closed total force is zero... so force felt by arbitrary shape equal to negative of that felt by the straight line ab. which is a bit simpler to find..
dint see post 4
30We got the answers to both the questions.. I think both post#2 and post#4 are absolutely correct. To your earlier doubt, we can apply polygon law because we are considering any arbitrary loop, and we may consider that loop as a polygon of n dl sides.
30I think two is pretty justified. I dont know if post #4 means to sya this..
Let the force on the wire joining A and B be denoted by F.
F=\sum{i\vec{dl}\times\vec{B} }=i\vec{B}\times\sum{\vec{dl}}=i\vec{B}\times \vec{r} _{AB}\text{ ...[Again by polygon law]}}