62This one is a very good question...
no one trying?
1well, the idea here is whenenver the drop comes in contact with the sphere the charge of the drop is distributed to the outer surface of the sphere because the sphere is conducting....
so all that is to be done is to see that the (n+1)th drop arriving enters the small ole with velocity equal to zero.... after that gravity does the rest of the job..
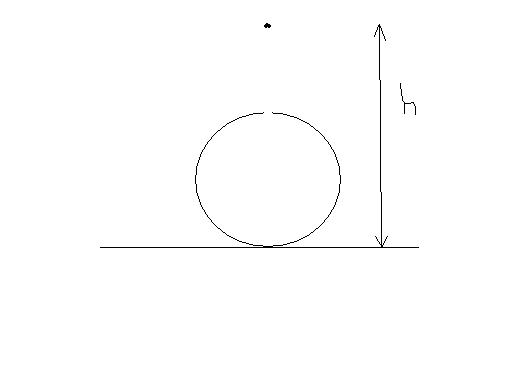
for the velocity to be zero, the change in kinetic energy between the 2 points is zero which implies that net work done =0 or work done by electrostatic force is equal to work done by gravity.
knq2(1/(h-R)-1/R)=mg(h-2R)
therefore, n=kmgR(h-R)/q2
n=4πε0mgR(h-R)/q2
1No Celestine, mr nobody is correct...he has taken mg(h-2R)...so, the minus sign cancels...
(i'm getting the same answer by a different (longer) approach...)
1
Shreyan
·2009-05-29 01:59:34
\Delta U = U_{f} - U_{i}
\frac{kQq}{R}-\frac{kQq}{h-R} = mg2R - mgh = mg(2R-h) = -mg(h-2R)
(dunno if i'm blabbering nonsense...arguing with a 45 ranker over tit-bits like sign problem!!!)
9haha
see
ΔUelectro = ΔUgravity is wrong
its actually
ΔUelectro + ΔUgravity = 0
1
Shreyan
·2009-05-29 02:22:51
ohk....got it...thanx a lot [4]..
(arguing with a 45 ranker does help!!!)
anyway...congrats 4 ur fabulous result!!
9
Celestine preetham
·2009-05-29 04:56:06
ya i used to argue a lot with nishant byah in my early tiit days and always learnt my silly mistakes !
1
Samarth Kashyap
·2009-05-29 17:09:41
thanx for the correction[1].......these small errors can cost u dear in JEE
