Electricity and magnetism - Method of Image charges

62

Lokesh Verma ·2011-06-15 02:45:50

Method of images is a classic example of how a result in mathematics is exploited in physics.

The basic funda is this.

If f'(x) is known and f(a) is known for some contant a, then f(x) is known everywhere.

a is called the boundary, if it is the end point or something.

Now, look at E and V

we know the relation between E and V

So if in 2 different situations, E is the same everywhere and if on the boundary V is the same then V will be the same everywhere....

(This is though not the 100% exact explanation but for ur level I guess this is the understanding that will help)

The remaining about how to find the potential.. Subhomoy will take care :)

UP 0 DOWN 0
Post on FacebookPost anonymously?

49

Subhomoy Bakshi ·2011-06-15 08:25:15

I ll try to give a write-up tonight! [1]

UP 0 DOWN 0
Post on FacebookPost anonymously?

49

Subhomoy Bakshi ·2011-06-15 12:50:08

Continuing after nishant bhaiya's post:

Consider the case below: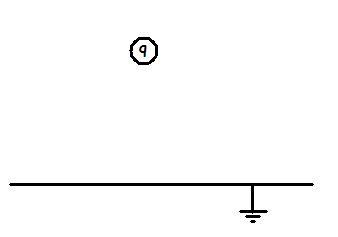

Question: find the attraction on the point charge q kept at a distance d from a grounded metallic plate of infinite dimensions...

Before we start solving the question, we need to understand one thing.. why will there be any attraction anyway????

the reason is the charge q induces a charge -q on the upper surface of the plate and the rest is neutralised due to grounding..now this net charge on the plate is the reason for attraction..! [1]

Next u need to realise that since we had grounded the plate, then we have a 0 potential throughout the conducting plate..
thus, the plate forms a equipotential surface...

you need to realise too that even if the plate wasnt grounded, we could have treated it as a spherical shell with radius=âˆž and so if it had a charge q' on it,
it's potential V=kq'âˆž=0
and metals are always equipotential surfaces! [1]

Now, since the plate is an equipotential surface, thus, the electric field lines must be perpendicular to it always (why?)

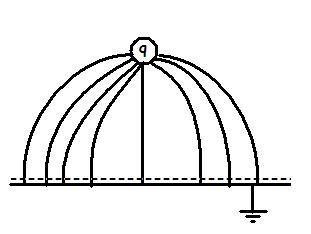
Now try to recollect the lines of force for a dipole: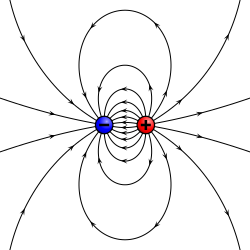

now see... the electric field lines drawn in the original problem case is exactly the right half of the field line

So we can consider our original case as a result arising from a dipole..

To do that what we do is consider the conductor as a mirror and at the position where the image of q should reside we put a -q charge..and we remove the conductor plate...

This regains original fields as they were in the original case and we can also find out the amount of force with which the point charge q gets attracted!

The resultant figure is somewhat like this: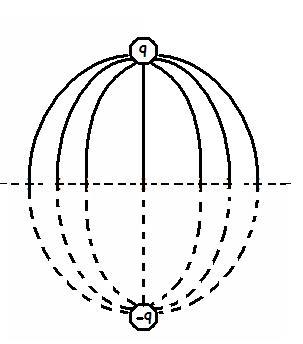

I have denoted the extension of field lines on to the bottom part by dotted lines since they do not exist in truth and i have denoted the original position of the metallic plated by the dotted straight line...

and the net force = kq²(2d)²=kq²4d²
[1]

UP 0 DOWN 0
Post on FacebookPost anonymously?

49

Subhomoy Bakshi ·2011-06-15 12:57:35

Quote from last post: "To do that what we do is consider the conductor as a mirror and at the position where the image of q should reside we put a -q charge..and we remove the conductor plate..."

Q: why is this valid at all???

ANS: just beause the points in which the electric field existed in the original case, those points still have the same electric field and potential after the alteration...

Same explanation could have been given using mathematics.. on the lines nishant bhaiya had started giving the explanation but I preferred to explain using electric field lines...though it indirectly means the same, still in physics we should think physics [6]..
On utmost need I can also give the mathematical explanation but this technique just has limited use, so lets put a full-stop here itself! [1]

cheers!

UP 0 DOWN 0
Post on FacebookPost anonymously?

21

Shubhodip ·2011-06-15 22:33:47

My answer to why this is valid at all:

Conditions to be fulfilled as mentioned above:

a)The potential all over the conducting plane must be zero.

b)The total normal electric displacement flux integrated over a closed surface is either 4Î q or zero,depending on weather the closed surface has an enclosed charge or not.(this is just gauss law)

c) potential at infinity is zero.

The solution (1) as suggested by Kelvin is consider the conductor as a mirror and at the position where the image of q should reside we put a -q charge.

It is easy to check that this distribution fulfills our conditions. By uniqueness theorem solution (1) is the only solution. The proof is like this: On the contrary let us assume that there exists another solution say solution (2) which satisfies the above conditions. Let us replace all the charges of the system by charges of opposite signs,call this solution (-2). This solution (-2) does not effect condition (a) and (c). But it violates (b), it makes the total normal electric displacement flux integrated over a closed surface is either -4Î q or zero,depending on weather the closed surface has an enclosed charge or not.Therefore ,if we superimpose solution (1) and (-2) the total electric displacement flux integrated over any surface is zero. So, solution (1) is opposite of solution (-2). Again solution solution (2) and solution (-2) are opposite. Therefore solution (1) and (2) must be same.This proves the uniqueness of our solution.