1ans is (B)
Two charges +q1 and -q2 are placed at A and B respectively. A line of force emanates from +q1 at an angle \alpha with AB. At what angle \beta will it terminate at -q2 ?
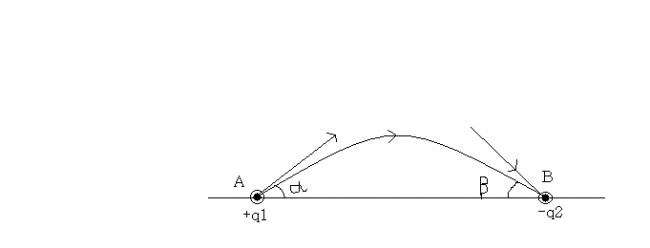
A) sin^{-1}[\sqrt{\frac{q_{1}}{q_{2}}}sin\frac{\alpha }{2}]
B) 2sin^{-1}[\sqrt{\frac{q_{1}}{q_{2}}}sin\frac{\alpha }{2}]
C) sin^{-1}[\sqrt{\frac{q_{2}}{q_{1}}}sin\frac{\alpha }{2}]
D) 2sin^{-1}[\sqrt{\frac{q_{2}}{q_{1}}}sin\frac{\alpha }{2}]
-
UP 0 DOWN 0 1 8
8 Answers
1see this post http://targetiit.com/iit-jee-forum/posts/aakash-aits-8-qsn-14198.html
341Hey, I had seen this qn in my student times! Its there in a collection of Russian Physics Olympiad problems by S S Krotov.
1use solid angle concept combined with the fact that flux leaving q1=flux entering q2
106@akari: why should flux leaving q1 = flux entering q2 ?? (im a bit confused at that part)
@bhatt sir: third time uve replied in a physics thread (if my memory is intact)
1http://targetiit.com/iit-jee-forum/posts/a-good-1-10144.html
Draw a gaussian surface such dat it allows flux leaving q1 = flux entering q2 and proceed.
1see the flux lines emerge from everywhere
so in 3D it foems a cone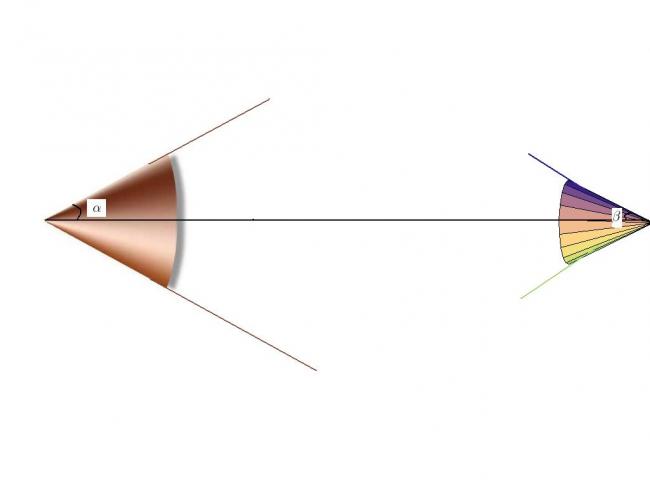
\text{solid angle }\Omega =2\pi(1-cos\alpha )\\ \phi(out) = \frac{q_1\Omega }{4\pi\varepsilon_0}=\frac{q_1 (1-cos\alpha )}{2\varepsilon_0}=\phi (\text{going inside q2}) =\frac{q_2 (1-cos\beta )}{2\varepsilon_0}\\ q_1\sin^2\alpha=q_2\sin^2\beta\\ \sin\beta=\sqrt{\frac{q_1}{q_2}}\sin \alpha