1given in hcv page no 146 -147
neways itz out of portion :)
Q. Two spheres of radii R1 and R2 are connected by a wire. What is the equivalent capacitance of this system
-
UP 0 DOWN 0 3 11
11 Answers
24if they are placed far apart....then they can be observed as capacitor(simple one)
34∩ε/(1/a+1/b-2/d) where a and b are radius of two spheres and d is the separation
1i had assumed vaccum as its media and r is the distance b/w their centres
i think thiz wuld be the answer
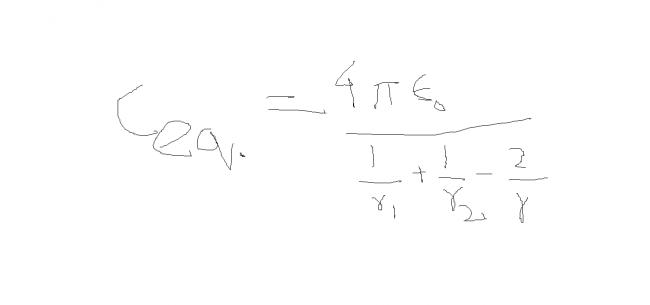
106OUT OF PORTION !!! i din kno.. can u tell me how u know that?
answer was given 4πε0(R1+R2)
66By definition, put some charge on the system and figure out the potential. The ratio is the capacitance.
I am going to assume that the spheres do not interact. If I put charge Q on the system, it will get divided between the two spheres. Let q1 and q2 be the charges on, respectively, the sphere with radius R1 and R2. Since the two spheres must be at the same potential, we get
q1/R1 = q2/R2
Additionally, q1 + q2=Q
Solving them we get
q1 = QR1/(R1+R2) and q2 = QR2/(R1+R2)
Hence, the common potential of the system
V=\dfrac{q_1}{4\pi\epsilon_0R_1}=\dfrac{Q}{4\pi\epsilon_0(R_1+R_2)}
As such the capacitance is
C=\dfrac{Q}{V}=4\pi\epsilon_0(R_1+R_2)
That's your answer.
106thanks sir.
sir can you please clarify on the formula written in above posts
#5,3
whether they are correct.
if they are correct what is the condition or restriction on them and how they are derived
66The above results will apply if we assume that the potential of each sphere is affected by the other (but still assuming that the charge distribution remains uniform on each sphere).
In this case, continuing my previous notations, the equality of potential give
\dfrac{q_1}{4\pi\epsilon_0R_1}+\dfrac{q_2}{4\pi\epsilon_0d}= \dfrac{q_2}{4\pi\epsilon_0R_2}+\dfrac{q_1}{4\pi\epsilon_0d}
Obviously we still have q1+q2 = Q
Solving for q1 and q2, we obtain
q_1=Q\dfrac{\frac{1}{R_2}-\frac{1}{d}}{\frac{1}{R_1}+\frac{1}{R_2}-\frac{2}{d}}
and
q_2=Q\dfrac{\frac{1}{R_1}-\frac{1}{d}}{\frac{1}{R_1}+\frac{1}{R_2}-\frac{2}{d}}
Hence, the common potential
V=\dfrac{1}{4\pi \epsilon_0}\left(\dfrac{q_1}{R_1}+\dfrac{q_2}{d}\right)=\dfrac{Q}{4\pi \epsilon_0}\cdot\dfrac{\frac{1}{R_1R_2}-\frac{1}{d^2}}{\frac{1}{R_1}+\frac{1}{R_2}-\frac{2}{d}}
which gives the capacitance as
C=\dfrac{Q}{V}=4\pi \epsilon_0\dfrac{\frac{1}{R_1}+\frac{1}{R_2}-\frac{2}{d}}{\frac{1}{R_1R_2}-\frac{1}{d^2}}
which reduces to the result I previously derived if d →∞.
66the formula given in #4 and 5 are not correct for the present situation.