answer given at the book is a terror...i will post it
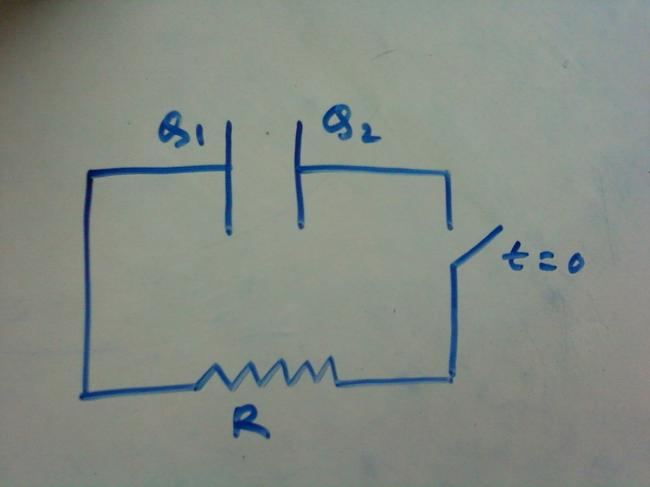
the two plates of a capacitor with capacitance C is given q1 and q2 charge,,the system is as shown where R is resistance..the key is closed at t=0 find charges on the plates after time t.
-
UP 0 DOWN 0 0 5

5 Answers
First thing to do here is to find the potential difference between the plates..
If one plate has chage q and other Q
What is the answer?
Then we will solve it fully.
potential difference: Q-qAεo.d
supposing:: 1)there is no fringing effect...i.e. i have considered infinitely long plates
2)the plates are close so that the electric field is uniform between them.
after the hnt from nishant bhaiya, i am solving this,
let after time dt, dq charge flows from Q to q.
so new charges on plate= Q-dq and q+dq
and i=dq/dt
V'=Q-q-2dqAεo.d
applying KVL,
V'-iR=0
Q-q-2dqAεo.d=Rdqdt
at last i read about charging in C-R circuits
at steady state charge on each cap. (q1+q2)/2
then at time t
q=(q1+q2)/2(1-e^- @t)
where @=(cR)