1i hv got the ques...........bt i ws jst arguing for wt i hd said.....i ws initially wrong[4]
may be the dumbest question one can give in arithmetic progresions
Let a,b,c,d be four distinct positive integers in arithmetic progression. Prove that abcd is not a perfect square.
-
UP 0 DOWN 0 1 19
19 Answers
1
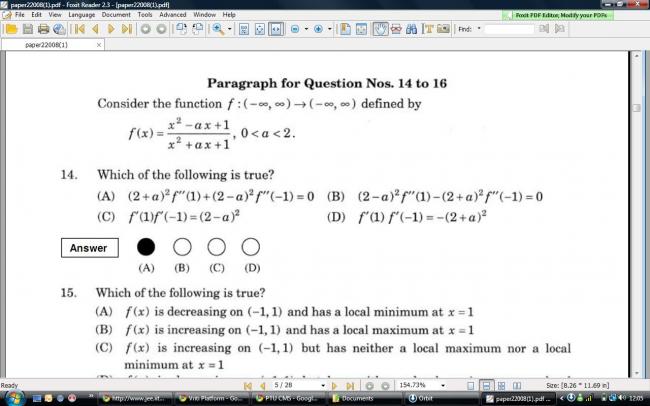
341the first line of the question is a howler, because if 0<a<2, then, both numerator and denominator are positive for all x, then how can it possibly have range (-∞,∞)?!!
f(x) = (x2-ax+1)/(x2+ax+1) = 1 - 2ax/(x2+ax+1)
= 1 - 2a/(x+1/x +a)
Let y = x+1/x.
Then the expression is 1 - 2a/(y+a).
Differentiating with respect to x, we get f'(x) = 2a/(y+a)2 y' = 2a/(x+1/x+a)2 (1-1/x2)
It is easy to see that f'(1) = f'(-1) = 0.
Differentiating again and remembering that y'(1) = y'(-1) = 0,
we see that f''(1) = 2a/(a+2)2 and f''(-1) = -2a(a-2)2 so that
(a+2)2f''(1) + (a-2)2f"(-1) = 0.
The derivatives obtained easily answer part 2 of the question also.
341Could you post the question, because I dont know which problem you are referring to?
1sir can u suggest any way to speed up the differenciaton speed.....bcoz last year one question was there in which we had to differenciate twice...to get the answer(it was in the paragraph)
341any equation of the form f(x1,x2,x3...,xn) = 0 with x1,x2,x3...,xn being integers.
ax+by = c
x2+y2 = z2 are examples
The most famous one would be xn+yn=zn
The result that this is not solvable in integers for n>2 is now known as Fermat-Wiles theorem.
11@prophet.
wats the Diophantine equations? I havn't learned them...
Can u put sum light over it...
341We have to prove that it is impossible to have
a(a+d)(a+2d)(a+3d) = n2
a(a+d)(a+2d)(a+3d) = (a2+3ad)(a2+3ad+2d2)
= (a2+3ad+d2-d2)(a2+3ad+d2+d2)
= (a2+3ad+d2)2-d4 = n2.
x2-n2=d4
But this is a corollary one of the Diophantine equations proved as insoluble in integers by Fermat.
Hence there exist no four consectutive numbers in arithmetic progression such that their product is a perfect square
1they are in AP
then let a=A
then b=A+D,c=A+2d and d=A+3D
so they cn't form perfect sq
62honey you are not getting the point of this question..
See if we have to prove that something is true (and it is) then how can someone give a counterexample!!!
1coz common difference always changes the next term..........so no 2 terms cn be equal nd to be a sq all sides mst be equal
13it'll b a perfect square only when a=b=c=d or a,b,c,d are perfect squares individually...
given that a,b,c,d are all distinct... so first case is ruled out...
n second case is obviously not possible, because no 4 perfect squares are in AP...
13let
a=p-3q ; b=p-q ; c=p+q ; d=p+3q...
abcd = (p2-q2)(p2-9q2)........... which cannot be perfect square anywayzzz... gottt...!!!
11Let a= x-3s
b= x-s
c=x+s
d=x+3s
Thus they form an AP
abcd= (x2-s2)(x2-9s2) --------(1)
I don't knw how to prove that (1) is not a perfect square.