draw the altitude on this equilateral triangle by drawing radius of these small circles.....
we get two similar triangles...
now apply .....sinA/a = sinB/b = sin C/c
sin30/2r= sin60/4
1/4r=√3/8
2/√3=r
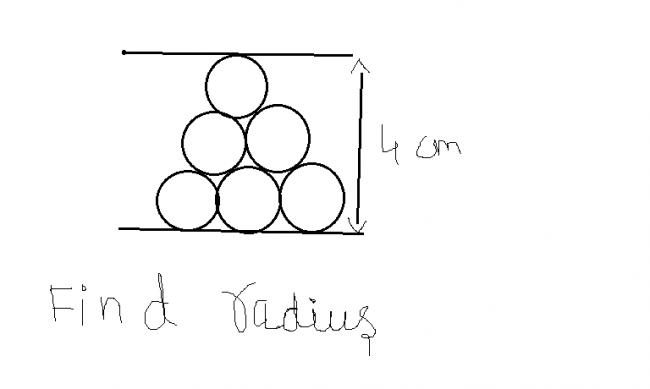
There are six circles of equal radius and are arranged as an equilateral triangle.
Find the radius of the circle.
Thanks Sir......Never thought about the height of the equilateral triangle in terms of sin
And rahul...Nishant sir's answer is rite.
Maybe its 4√3/9 .... not sure and confident as Nishant sir's answer is quite different.
draw the altitude on this equilateral triangle by drawing radius of these small circles.....
we get two similar triangles...
now apply .....sinA/a = sinB/b = sin C/c
sin30/2r= sin60/4
1/4r=√3/8
2/√3=r
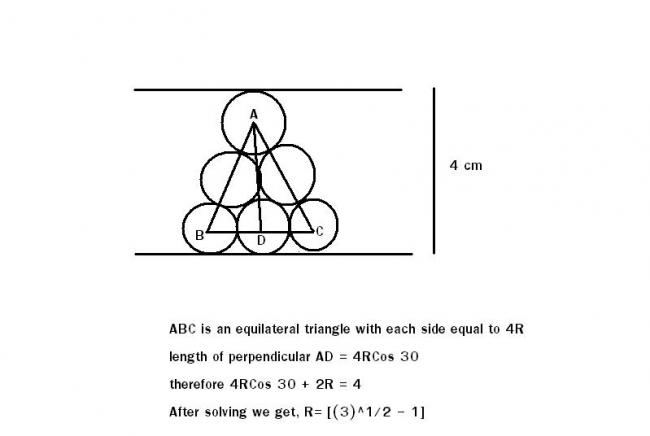
So R = √3 - 1
check that there is a slight mistake in nishant sir's calculation......
.....sinA/a = sinB/b = sin C/c
sin30/2r= sin60/4-2r
1/4r=√3/[2(4-2r)]
8-4r=4√3r
8/4√3+4=r
r= 2/√3+1 r= (√3-1)= ans....
@ venketesha ... u have made mistake in calculations dude....
U MADE THE same mistake as i did in my earlier post ... the height is 4-2r and not 4..see the figure carefully.........
The answer in √3 - 1.........Nishant Sir just made a very small mistake in the last step
And rahu....l......The height of the right angle triangle u have drawn in not 4......
It is 4 - 2r