341check if the function constructed by you is continuous.
You can easily construct more examples.
Take: f(x) = x if -1≤x≤1,
= 2 -x if 1 ≤x≤3
f(x+4) = f(x)
And now consider g(x) = e|x| f(x)
Is it possible to find a continuous function defined over all real numbers such that its graph intersects any non-vertical line in infinitely many points?
-
UP 0 DOWN 0 0 21
21 Answers
341There is a function satisfying the criterion, in fact infinitely many.
BTW, the function f(x) = sin x is a counterexample to your conjecture isnt it?
Chinmay's post offers a good starting point
341
21yup sorry
f(x) = lima→∞(ax sin x) works..
same concept as e^|x| sinx
is der any other type of function? i.e w/o sine?
341To add to aditya's wonderful example we look at how many solutions we have for
mx+c = e^{|x|} \sin x
or e^{|x|} \sin x - mx = c
For large enough n, if we consider the points
x = (4n+1)\frac{\pi}{2}; (4n-1)\frac{\pi}{2} the function oscillates from a negative number of large magnitude to a large +ve number.
By IMV it has to take the value c at some point between these two.
Further we will obtain solutions for all N≥n so that now we have infinitely many intersections with the line y = mx+c
[@ Arnab it means all non-vertical lines. Otherwise chinmay's example was good enough.]
262@arnab- you are mistaken. the problem is to find a function such that it intersects ANY straight line at infinite points (non vertical). i.e. y=mx+c where m,c are parameters should intersect at infinite points
21Completely misunderstood , thought any = all
Here is a simpler function
f(x)=x+ sin x
and its easy to see/prove that it intersects y=x at infinte points.
edit: log in problem :D
262i dont have any proof other than geometrical interpretation.
the fact is that the amplitude of the oscillation increases exponentially whereas the slope of the str. line is constant.
here is the graph for better understanding-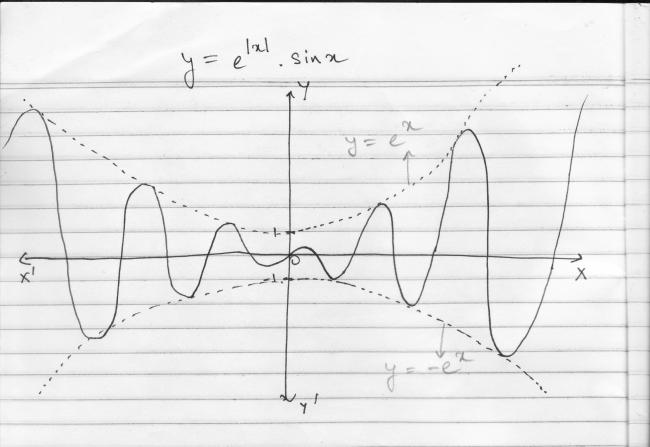
11oops - I was trying to prove there cannot exist any function intersecting all nonvertical lines at infinitely many pts; [3]
1Ofcourse!
take f(x)=sin x and the non-vertical line as y=some legitimate k like 0.5(say) and you are through!
11@ prophet sir,
I've a proof, but interestingly that is including another thing - my proof says there cannot exist any function intersecting any non-vertical line even twice!
Can you pls confirm if that's correct or not.
1oops ive made a mistake with intervals
should include -1 and 1 in any of the 2
341Guys, please attempt to substantiate your claims. That itself will weed out several guesses
262what about y=Asinx where A→∞ ?
any non-vertical line will be cut infinite times
1let the line be: y=x
and the function be y=|x| for all x e (-∞,-1) u (1,∞)
=x2 for all x e (-1,1)
21if its like this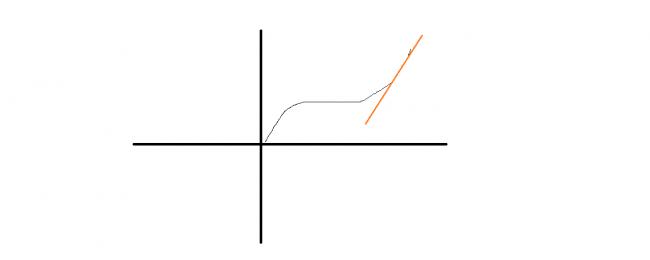
i think it is possible
but if its like this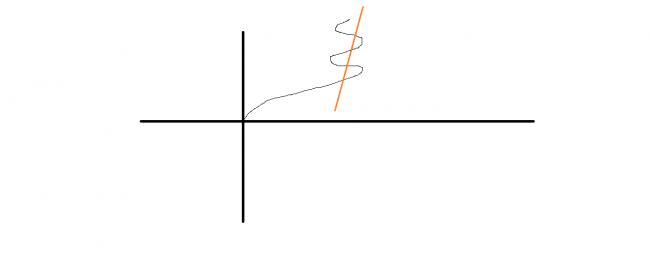
it is not a function at all.
1Hmm....I am able to think of a couple of functions continuous over their domain which intersect any non-vertical line at infinitely many points.
I doubt if it holds for any continuous function over entire real line...