Let f be a function from the set of points in the plane to the set of real numbers ,with the property that for any square ABCD,
f(A)+f(B)+f(C)+f(D) = 0
Prove that f(P) = 0 , for any point P in the plane.
Not a doubt.
-
UP 0 DOWN 0 0 2

2 Answers
[2] This is a q from putnam 2009.
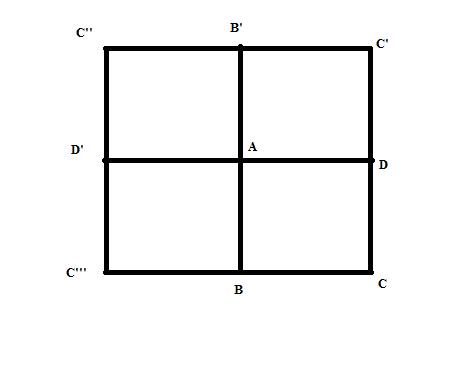
Take any point A in plane. we will prove f(A) = 0
We have from the construction in figure
[f(A) + f(D) + f(C') + f(B') ]+ [f(A) + f(B') + f(C'') + f(D')] + [f(A) + f(D') + f(C''') + f(B)]+[f(A) + f(D) + f(C) + f(B)] = 0
=> 4 f(A) + [f(C) + f(C') + f(C'') + f(C''')] + 2[f(B) + f(D) + f(B') + f(D')] = 0
But from figure [f(C) + f(C') + f(C'') + f(C''')] = 0, [f(B) + f(D) + f(B') + f(D')]= 0 ( they r also squares)
this gives f(A) = 0 [1]