24(m+n-2)!(m-1)!(n-1)!
A person is to walk from A to B. However he is restricted to walk only to the right of A or upward of A, but not necessarily in this order.
in the figure there are m vertical and n horizontal lines. Determine the total number of paths available to a person from A to B.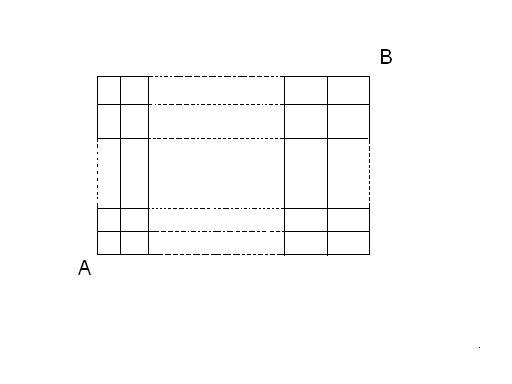
-
UP 0 DOWN 0 1 9
9 Answers
24take an alementary case and try urself....for eg 3 horz lines and 4 vertical lines...
11I think Catalan numbers can better settle this.....I shall try to prove it, but the problem is I'm not very good at the same.....Shall try 2 give it by Monday.
1suppose,u are going vertically upward n reching left top corner n den turning right...so,u hav to move (n-1) boxes up,n den (m-1)boxes right.....so d answer is [(m-1)+(n-1)]!/ (m-1)!*(n-1)!
62soumik.. dont bring in catalan number.. that is something very different...
Here the number of ways is as given by eureka in post 2
Basically you have to take m-1 steps horizontally and n-1 steps vertically.
So you have to take m+n-2 steps in all and you have to decide which of these have to be horizontal and which have to be vertical...