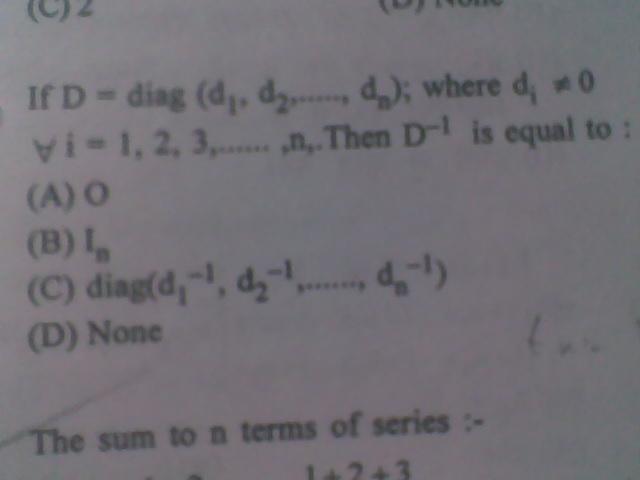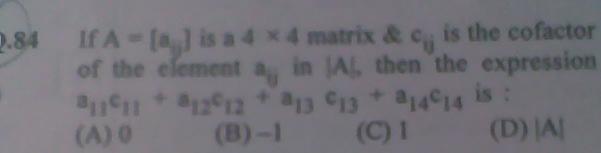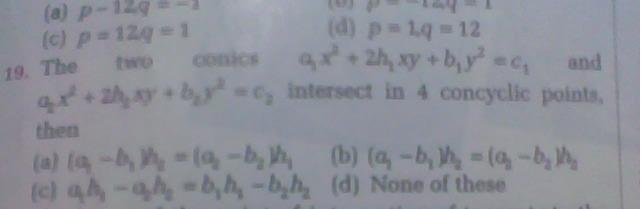\frac{x^{4}}{(x-1) (x+1)^{2}}
=(x-1)+ \frac{2x^{2}-1}{(x-1)(x+1)^{2}}
[3] please show the divison process .. when num was divided by denom.. got the 2nd step.. pls show step wise how it occured
1° The inverse of diag [ d1, d2, ... dn ]
is diag [ d1-1, d2-1, ... dn-1 ]
so, option (C)
° next Q ...
a11c11 + a12c12 + a13c13 + a14c14 = | A |
{ dats how u evaluate determinants na }
option (D)
° Above Qsn -
no. of subsets of a set with X elements is 2X
so, condition is 2m = 56 + 2n
a lil bit of trial and error with powers of 2 will give u tht it shud be
64 = 56 + 8
So,
m = 6
n = 3
1P & C question
4 digit numbers with 5 in units place
_ _ _ 5
1,3,7,9 can be arranged in these places in 4P3ways
Answer is 24
1396.
after dropping the first card...the second card should be one of other 3*13=39 cards
sample space 51 cards as 1 has been dropped.
so ans =39/51=13/17
13?00....2n boys divided...
ans n/(2n-1)
Let there are n seats in two groups
T1 is seated in a seat ... so there are now 2n-1 seats left....among which n seats are in the other group...T2 can be seated in any of the n seats
1Quest 107
Let the number of ways of selecting the atmost n things out ou 2n+1 things be K
K= 2n+1C0+2n+1C1+2n+1C2+...................................+2n+1Cn-1+2n+1Cn
2K=2 (2n+1C0+2n+1C1+2n+1C2+...................................+2n+1Cn-1+2n+1Cn)
=2n+1C0+2n+1C1+2n+1C2+.............................+2n+1C2n-1+2n+1C2n+2n+1C2n+1
=22n+1
K=22n
Given that K=256
K- 2n+1C0=255
2n=log2256
=8
Therefore, n=4
I took K=256 and not 255 because the question has ignored the event of not selecting Anything,which can be done in one way!
[339]
1two finite sets have m and n elements respectively. The total number of subsets of first set is 56 more than the total number of subsets of the second set. the values of m and n respectively are_____________ ?
show me the solution please
1
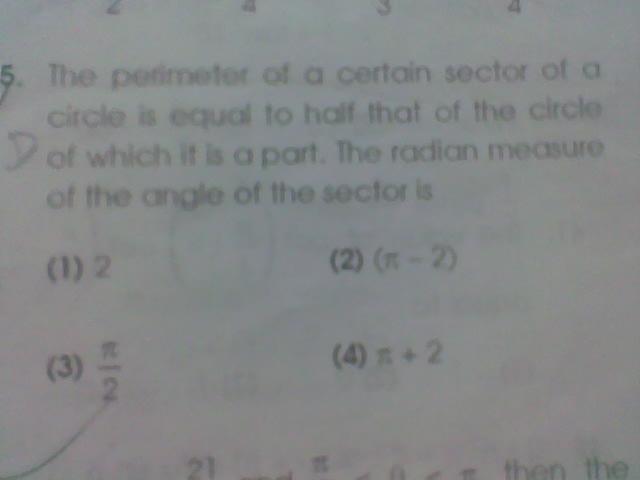
let the radius of circle be r and @ be angle of sector
we have according to question
r@+r+r=2pi r
@=pi-2
so ans is (2)pi-2
1Thanks Mirka [1]
can u say
\in BINARY operations it says like
n(AxB)
ELEments are 2n2
can u show how ?
1equation of a citcle passing through the pts of intersection is :
a1x2+b1y2+2h1xy -c1+ λ(a2x2+b2y2+2h2xy-c2)=0
solve it to get the value of λ
(1. coefficient of xy=0
2. coeff of x = coeff of y)
11Is this not a simple binomial distribution sum??
n=7
p=1/2
q=1/2
r=4
but u'll get 35/128.........so please point out my mistake
1abhi... how do u get dis 6C3*(1/2)^6*1/2=5/32???
pls temme ..
12-1sol
x4-1+1 / (x2-1)(x+1)
( x2-1)(x2+1) / (x2-1)(x+1) + 1/(x2-1)(x+1)
( x2+1) / x+1 + 1/(x2-1)(x+1)
(x+1)2-2x / x+1 + 1/(x2-1)(x+1)
x+1 - 2x/x+1 + 1/(x2-1)(x+1)
x-1 +2 - 2x/x+1 + 1/(x2-1)(x+1)
( x-1) +(2x2-1) /(x2-1)(x+1)
this your required proof
11. 10^{n}+ 3(4^{n+2})+5
is divisible by __________
a>13 b>9 c>11 d>12
2. if n is a natural number then (\frac{n+1}{2})^{n}\geq n!
is true when
a>n≤0 b>n≤1 c>n≤5 d>n≥9
1but mr.manipal it is n<=5, n=5 is satisfyin but wat about 0 wich is less than 5........[:)]
62if n is a natural number then (\frac{n+1}{2})^{n}\geq n!
is true when
(1+n)/2 > (1.n)1/2
(2+n-1)/2 > (2.n-1)1/2
(3+n-2)/2 > (3.n-2)1/2
....
....
...
...
so we have got...
(\frac{n+1}{2})^{n}\geq n! for all integers...
See fi this makes sense :)
