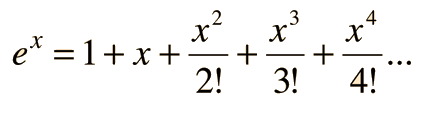11i didn't get u mani
see the expansion of ex is
e^x=\sum_{n=0}^{\infty}{\frac{x^n}{n!}}
so for x=0, why Doesn't that expansion hold good?
ex is defined as
e^x= \frac{x^0}{0!}+\frac{x^1}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+..........
for x=0,
e^0= \frac{0^0}{0!}+\frac{0^1}{1!}+\frac{0^2}{2!}+\frac{0^3}{3!}+..........
but we know that e0 is 1
So
1= \frac{0^0}{0!}+\frac{0^1}{1!}+\frac{0^2}{2!}+\frac{0^3}{3!}+..........
1=0^0
What's the folly??
-
UP 0 DOWN 0 0 11
11 Answers
11the expansion is ex is alway written as
e^x= \frac{1^}{0!}+\frac{x^1}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+..........
And not
e^x= \frac{x^0}{0!}+\frac{x^1}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+..........
11No da x0 is always simplified and written as 1 for convinience
anyways, the source is reliable.....i doubt if u cud get a more reliable source than wiki
http://upload.wikimedia.org/math/0/b/c/0bc08045195dc823c22d1fa283cb0759.png
11http://www.math.com/tables/expansion/exp.htm
have a look at this 1
the 1st 1 u r making mistake in
and u r confusing between the 1st and the 3 rd 1
hope this could help
11
11Why are dodging the original definition??
ex= x0/0! + x1/1! +x2/2! + x3/3! + ................
And haven't we learnt that (cos90°).(tan90°)≠1 even though sin90°=1??
11even though we can cancel the two cos90°s??[5][5][5][5][5]
bHAI JO PEHLI DEFINITION DI HAI WOH ORIGINAL HAI
PEHLE TU YEH BATA
KI
TU PAANGE LE RAHA HAI
YA
FIR
YEH TERE POTENTIAL OUTSTANDING AND OUT OF THE WORLD BRAIN KI KHOJ HAI[7][7][7]
11allright allright...........sorry for the poor English
edited it now and so i implore thee to answer my question
apun ki brain ka khoj baadh me karenge