11)
d2Y/dX2=a/p2=M-2L-1
This raised to half gives, M-1L-1/2
Answer, A
[339]
1)if Y represents acceleration and X momentum,then the dimension of (d2Y / dX2 )1/2 is ???
A) M-1 L-1/2 T0
B) M L1/2 T-1/2
C) M-1 L1/2 T1/2
D)M0 L1/2 T1/2
2)the position vector of a particle is given by r=r0(1-αt)t ,where t is the time and α is a scalar constant and r0 is a constant vector. Then
A)distance covered in forward journey is |r0| /(2α)
B)distance covered in backward journey is |r0| /(4α)
c)total distance covered is |r0| / (2α)
D)the particle will come to starting point at t=1/ (2α)
3)the radii of the front and rear wheels of a carriage are a and b respectively and c is the distance between the axles. A dust particle driven from the highest point of the rear wheel is observed to settle on the the highest point of the front wheel. The velocity of the particle with respect to the carriage is
a)√g √(c+b-a)(c+a-b) / √4(b+a)
b)√g √(c+b+a)(a+b-c) / √4(b-a)
c)√g √(c+b+a)(c+a-b) / √4(b-a)
d)√g √(c+b-a)(c+a-b) / √4(b-a)
-
UP 0 DOWN 0 1 6
6 Answers
1
12)
The particle has an initial velocity of r0
The particle has an acceleration of -2αr0
The distance covered by the particle in the forward journey is r0/4α,
In the backward journey, the particle never stops, so the distance covered is ∞
The distance covered by the point before coming to its initial point is r0/2α
The particle returns to its initial position in time, 1/α
So, none of the options are right, in true sense.....
But if U consider the journey only till the particle comes back to its initial point, C can be marked right
[339]
13)
Firstly, for the particle to fall on the front tyre a<b
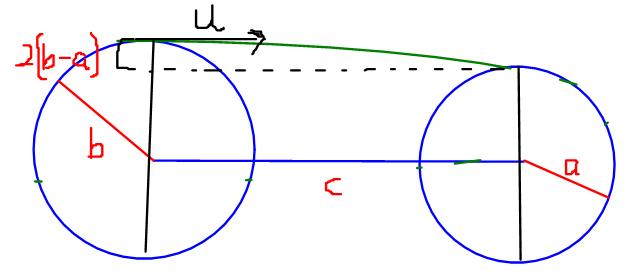
Let the particle have a horizontal velocity of u,
Using Newtons Laws,
Horizontally,
c=ut
=> t=c/u
Vertically,
2(b-a)=gt2/2
Equating the two, 2(b-a)=(g/2)(c/u)2
Or u = √gc2/4(b-a)
[339]