6ans.
(a)angle fromvertical is θ=30.??
(d)the angle at wich it loses contact is tanθ=2??
are the radial acc.=gcosθ
and tangentialacc.=gsinθ??
pls verify...
a point mass m starts from rest and slides down the surface of a frictionlesssolid sphere of radius r as shown in fig.(a)measur angles from the vertical and P.E.from the top(b)change in P.E.of the mass with the angle(c)K.E. as a function of angle(d)angle at wich it leaves contact(e)if there is friction wwat will happen??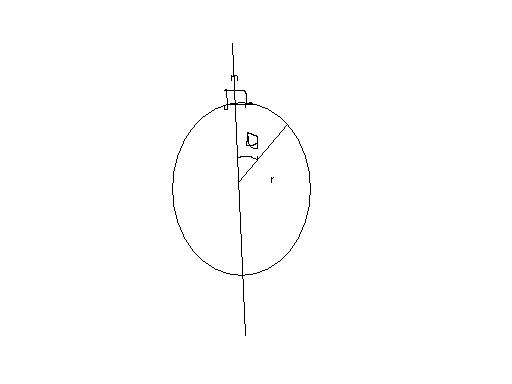
-
UP 0 DOWN 0 1 13
13 Answers
6
1have a doubt................in first part we have to find the angle travelled while the mass loose contact na(widout friction)..........
1if m getting the question right...then the answer to first part m getting is====cos inverse 3/4
1velocity at theta angle m getting is ......vtheta2=gR{(9/4)-2cos(theta)}
1just put the theta nd nd u will gett the vel. and K.E..................if m right
6are the radial acc.=gcosθ
and tangentialacc.=gsinθ??
6pls somebody check the ans given by me......n help me in the frictional part.
6in the frictional part the block will not leave the contact where is sud hav done if friction was'nt there.it will leave contact somewhere after that paricular point????