HELP
Suppose a circular string with linear mass density U and radius R rotates with an angular speed W.A pulse moves on it with some velocity
Establish v = WR ( where v means the velocity of any point on the string)
-
UP 0 DOWN 0 0 9

9 Answers
that's the velocity of the pulse ; See what u hav to prove btw thnx for replying//
Actually you have to show the establish basic equation of circular motion ie v = rw
with help of a pulse travelling on it ...
but u can use the fact that C.P accn = mw^2 r
From the question given,it looks like initially the string was rotating and then with the help of something a pulse was rotated?
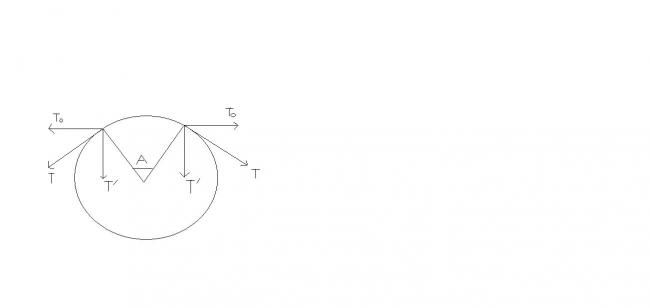
Let , angle A = dθ ,
v = ω R = velocity of the string ,
dl = differential length of the string ,
T 0 = T cos dθ2 ,
T ' = T sin dθ2 ,
Centripetal Force , F c = T ' + T ' ≈ 2 T . dθ2 = T dθ = [ U ( dl ) ] v2R
Since dθ → 0 , hence , sin dθ2 ≈ dθ2
Hence , T = U v 2
Consequently , Required velocity = ( TU ) 1 / 2 = v = ω R