9ok its a kind of implicit
32 Answers
62yes perfect celestine..
so it gives a contradiction to our assumption that
[x]=n
62see the answre is
n+sin n (for all integers n such that sin n is positive. )
If sin n is -ve there will be no solution... :)
Can you reason out why the above is true.
9hmm post 13 still pinked ?
nishant sir see #17
also even when positive can u guarentee [n + sin n] =n ???
what if sin n is negative
1found some solns
sin n +n
0,
1.84,
2.909,
3.14,
etc........
if x lies b/w(2n\pi ,(2n+1)\pi )
den
der would be 3 soln for every value of n
in d other region sin x<0 no soln
11thats y the disscussion is goin on
TO FIND A SEQUENCE
nishant sir thinks (have ) a sequence
but we don't think so
check whether u may prove to be useful
1just consider LHS &RHS seperate function &superimpose dem
werever both d functions intersect they bcomz d soln
y=\begin{Bmatrix} x \end{Bmatrix}
z=sin[x]
den plot dem
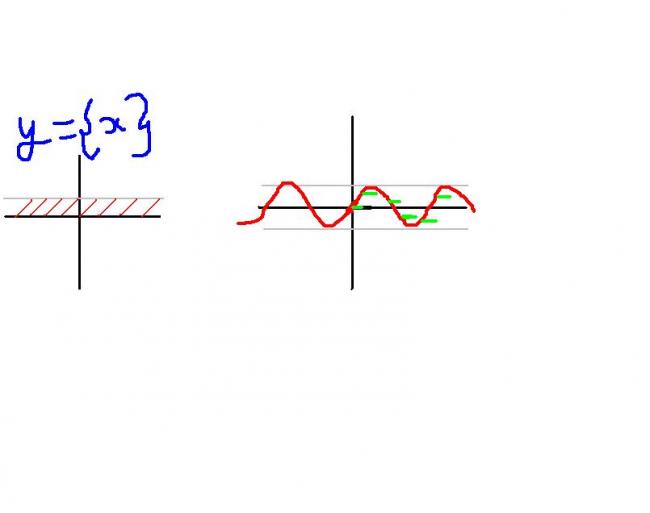[/img][/img]
a little more in nxt post
9its not n+ sinn chk for -1
also theres a lot of other things nishant bhaiyya has overlooked
1bhaiyya
what about n = 6 in
n+sin n
LHS is positive RHS is negative !
62yes celestine
the graph will be lines parallel to the y axis passing thru the points
n+ sin n
9byah is there a graph ?? see abv post
also i know the solutions
1yes
n +sin n
exactly
especially bcos sin(n) will never belong to N
62yes celestine
In the hind sight it should not have been on the graph of the day...
And yeah philip the answer is quite straight forward
x = n+ sin (n) for all integers n :)
1i think its quite straightforward !
sin 2 = 0.034899496702500971645995181625333
so x = 2.034899496702500971645995181625333
similarly
for all further values
i dont know how to do without a calc
ofcourse we have to neglect places where sin goes -ive
11celestine, the graph will be of the form x=k.....lines parallel to the y-axis
9why is this posted in Graph of the day ???
we cant draw graphs out of abv question as y is not invlolved
btw do u want us to find the solutions of x ??
11Notice that RHS and LHS are independent of each other! (Or are they?)
[7][7][7]
62anirudh you have done most of the hardwork already!!
Notice that RHS and LHS are independent of each other! (Or are they?)