1hehhe :)
this is the simplest looking graph ever given in GOD :)
12 Answers
21symmetric abt x=y;
passinm thru orig.
discontinuit at x=1 and at y=1;
y=x/(x-1);
y<0 for 0<x<1
+ve for the rest
1bhaiya,,, u wanted to gv this only naa ??
aur kuchh mod ya bracket ka galti ho gaya ?? :P
106y=x/(x-1)
dy/dx = -1/(x-1)2 which is always negative
d2y/dx2 = 2/(x-1)3 which is positive when x>1 and negative when x<1
at x=1 function is not defined as y=1+y ==> 1=0.... but at x=1- y=-∞ and at x=1+ y = ∞
at x=∞, y≈1
at x=-∞, y≈1
firther graph passes through origin..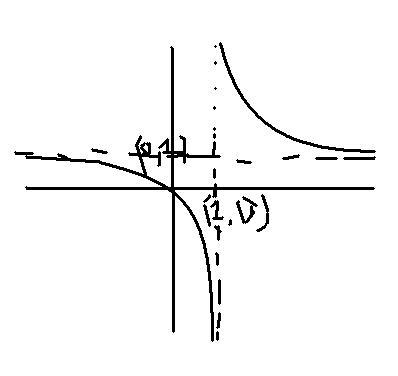
11it passes thru origin
but if we will write it as y=x/x-1 we can conclude that x=1 is its asymptote
and at x=2, y=2
taking its derivative
∂y/∂x=-1/(x-1)2 which is always negative
we can conclude that it is a decreasing f(x)
it is concave up for x>1 and concave down for x<1
I HOPE THAT THE PICTURE IS CLEAR NOW
62@sky: arrey most graph of days are simple only
if you did not notice.. there are hardy any graph of the days that have been put in the classics. So that must give you an idea too :)
@ asish, tapan and manipal: Good work guys :)
62The link is on your homepage
http://targetiit.com/home.html
the direct link is given by http://targetiit.com/iit_jee_forum.html?latest=6