Sorry i totally forgot that in {x} there is no negative part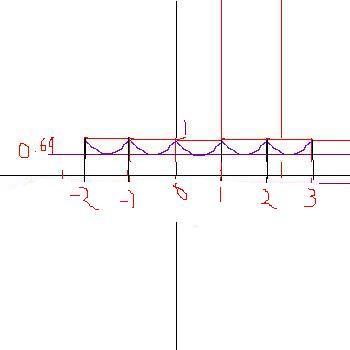
{x}{x} ≤1 if x>0
For 0<x<1
y = xx
if y(xx)>x
log y =x log x
dy/ydx= 1 + logx
0 = y + y logx
0 =1 + logx
log x = -1
x = 1/2.72
x = 0.367 it it the minimum
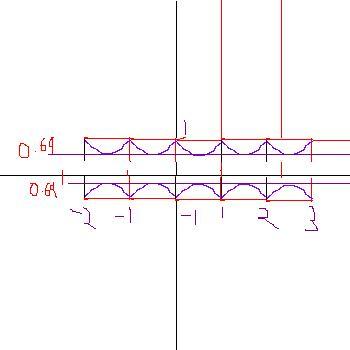
y = 0.69 minimum
Sorry i totally forgot that in {x} there is no negative part
{x}{x} ≤1 if x>0
For 0<x<1
y = xx
if y(xx)>x
log y =x log x
dy/ydx= 1 + logx
0 = y + y logx
0 =1 + logx
log x = -1
x = 1/2.72
x = 0.367 it it the minimum
y = 0.69 minimum
y=xx in the interval [0,1)
y>0
let y=lim(x->0){x}{x}
lny = lim(x->0){x}ln{x}
lny = lim(x->0+)lnx/(1/x) using LH rule
lny = lim(x->0+)(1/x)/(-1/x2)
lny = 0
y = 1
f(0+) = 1
f(1-) = 1
f'(x) = xx + xxlnx = xx(1+lnx)
f''(x) = xx(1+lnx) + (1+lnx)2xx + xx-1
= xx-1[(1+lnx)(2+lnx) + 1]
= xx-1[3+3lnx+(lnx)2] > 0
f'(x) >0 when 1+lnx>0 i.e. lnx > -1 i.e 1>x > 1/e
f'(x) <0 when x<1/e
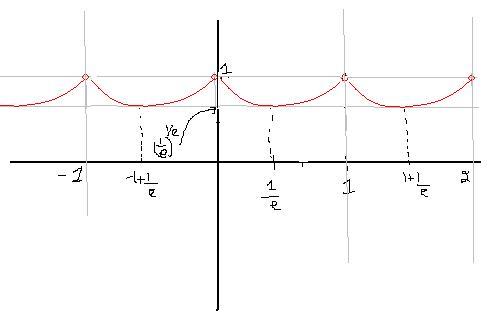
the limit would be 1?
because in 0-1
{x}=x
so it is equivalent to Ltx→0xx
You are right mani in saying that the values wont exist at the integers...
but the other analysis on your graph I am not very convinced!
sir
AM I WRONG IN SAYING THAT WE WON'T HAVE A VALUE OF THE FUNCTION AT THE INTEGERS
OR
THE VALUE EXISTS?????????/
This I thought was very easy! :O
Ppl did the other one.. but not this one :O
{x}{x} ≤1 if x>0
For 0<x<1
y = xx
if y(xx)>x
log y =x log x
dy/ydx= 1 + logx
0 = y + y logx
0 =1 + logx
log x = -1
x = 1/2.72
x = 0.367 it it the minimum
y = 0.69 minimum