@abhi double derivative check kar le yaar
17 Answers
sorry for the mistake
now i got it
THANX FOR THE HELP
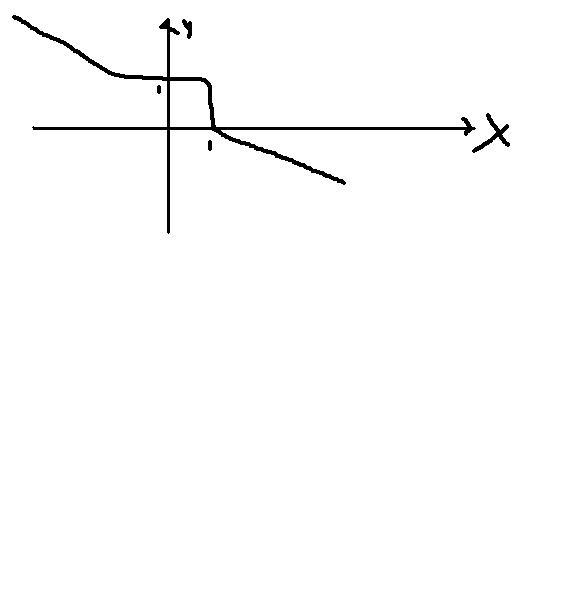
BUT SIR R THE PINKED GRAPHS PERFECT[7]
@mani,
the second derivative is
y^{\prime\prime}=-\dfrac{2x}{(1-x^3)^{5/3}}
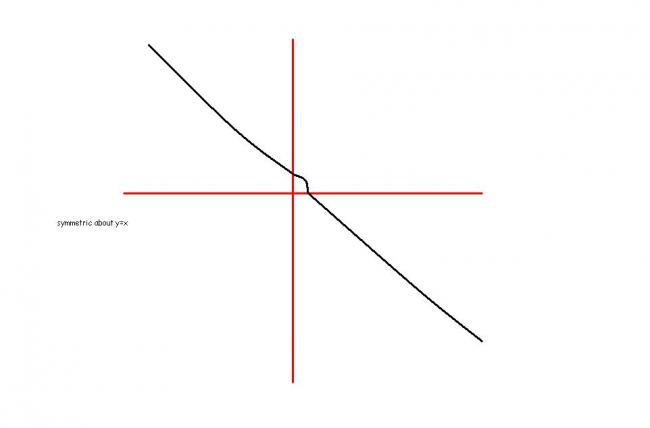
Now how are you getting the second derivative equal to zero at x=-1? In fact, as can be seen that for 0<x<1, the second derivative is negative (meaning the the graph is concave in this region), while for the rest of the region, it is positive (so that the graph is convex).
You can additionally determine the asymptotes. Since \lim_{x\to \pm \infty} y =\mp \infty, no horizontal asymptotes exists; similarly the function is not infinitely large for any real x<\infty, therefore no vertical asymptotes. Finally, we note that \lim_{x\to \pm\infty}\dfrac{y}{x}=-1, and \lim_{x\to \pm\infty}(y+x)=0, and so the only asymptote is the line x+y=0.
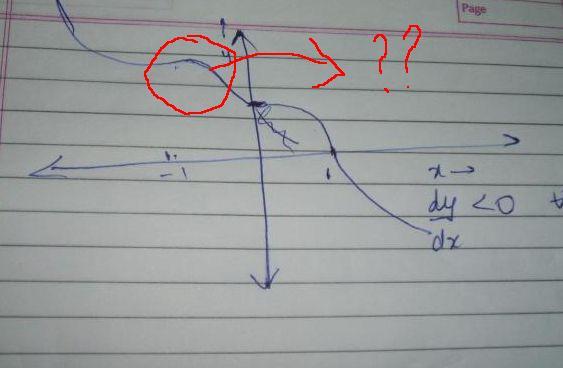
PLEASE DO TELL ME MY MISTAKE
DOUBLE DERIVATIVE WAS GETTING 0 AT X=+1 AND X=-1
I THOUGHT MY GRAPH TO BE AS POST 5
wahi.. when i gave
xn+yn=1 then not one person answered..
for n=3 everyone is giving answers..
Moral of the story: Stop fearing N and generalisations.
Roots=>y=0 =>x=1
Y intercept =>x=0 =>y=1
3x2+3y2y'=0
=>y'=-x2/y2
y'=0 =>x=0=>y=1
y'=∞ =>y=0=>x=1
y=1 ke pahle thoda smooth curve hoga naa ki straight........main theek kar ke post karta hoon
when x>1.then..y<1...that part is in 4th quardrant
and it is decreasing...
when y>1..then x<1....that part is in 2nd quadrant
when 1>x>0....and 1>y>0
only...then the curve is in 1st quadrant