11 soln. dat way..
Q Draw the graph of Total number of solutions of x2-2-2[x]=0
-
UP 0 DOWN 0 0 13
13 Answers
106we get x2-2 = 2[x]
So, x must be an integer.
So, [x] = x
SO,
x2-2x-2=0
==> x=(2±√4+8)/2 which does not give any integral values of x.
SO, NO SOLUTION
edits:
one solution. only
the mistake i had made was that x2 must be an integer. This does not imply that x must be an integer. x can be be √k where k is a whole no.
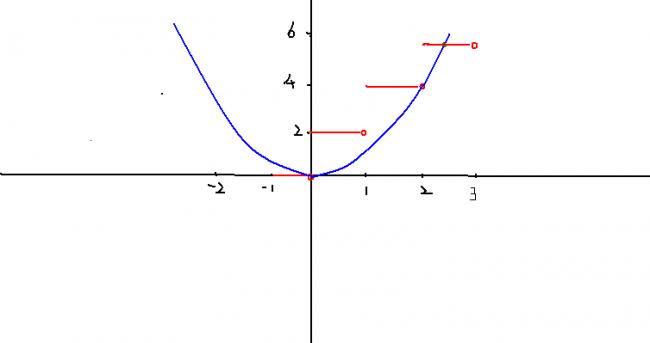
From gordo's graph (perfect),
we see that x lies in (2,3) so [x]=2
So, x2 = 2 + 2[x] = 2+4 = 6
So, x = √6 is the only solution of this equation.
1x2-2-2[x]=0
x2-2=2[x]
x2-2/2=[x]
This is graph of x2-2/2 and [x]
Hence it has one solution
*edited
11HONEY UR ANSWER IS WRONG .
gODO PLS GIVE THE ANSWER ACC TO U [1]
1#2 nd #3 are differnt.............which one is correct
n wtz wrong in my ans?
1:O
****we get x2-2 = 2[x]
So, x must be an integer.********
how u can say that ashish??
see if x is some square root of a integer ,even then ..............
correct me if i am wrong
106yup my mistake. edited that. the answer is one solution and x=√6 is the answer as in #2
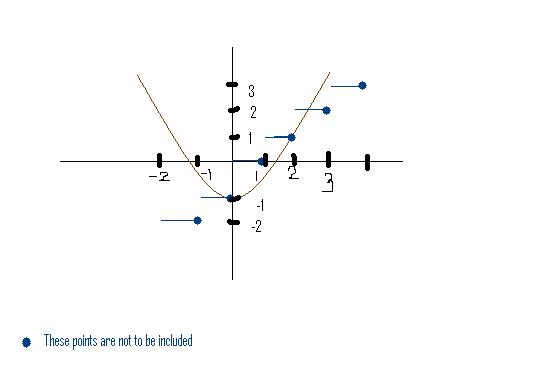
1Actually i hd put the same graph earlier even bt just forgot to mark the points....