1|xsin{x}|<=|x|
so graph lies b/w y=x&y=-x
is ma approach right?
12 Answers
1
62yes rip.. see carefully there is a mistake.. infact 2 major ones..
11sorry sir i did y =sin{x} earlier
Now for y=x sin{x}
we have to check it like from (0,1) it would be x sin x and from (-1,0) it would be x sin x+1
So it graph mite be
Analyzing x sin x =y
so
y'=sin x + x cos x >0 (0,1)
y"=cos x + cos x - x sin x >0 from (0,1)
and
y= x sin (x +1)
y'=sin(x+1) + x cos(x+1)
y"=cos (x+1)+cos(x+1) - sin(x+1) >0 (-1,)
so its graph could be like shown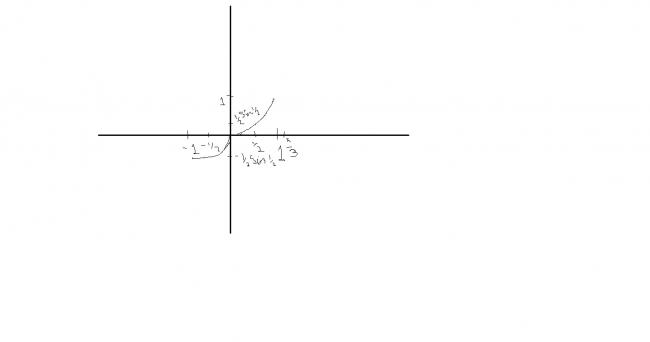
3mani in the graph all the values of y shud be positive since x and sin{x} are all positive
3y=xsin(x-[x])
y'=sin(x-[x])+xcos(x-[x]) >0 for all x >0 and is <0 for all x<0
we have continuity at x=0 so we will have a minima at zero.
And the graph has discontinuity at all other integer pts bcos {x}=0
i think with these we can draw the reqd graph.
11bhai msp
when we take x -ve then x will be negative and sin{x} will be positive
check it out
11[11][11][11][11][11][11]
can {x} be negative at any value
[11][11][11][11][11][11]