For The graph between (0,1) There will be no graph 0/x =0
For (1,2)
[x] = 1 which is a constant
let u = {x}
y = 1/u
yu = 1
This the graph of the rectangular hyperbola with lowest value 1
For (2,3)
y = 2/u
yu =2
it is also a hyperbola with lowest value = 2
For (-1,0)
y = -1/u
yu = -1
it is also a hyperbola with highest value = -1
For (-2,-1)
y = -1/u
yu = -2
it is also a hyperbola with highest value = -2
For (-3,-2)
y = -1/u
yu = -3
it is also a hyperbola with highest value = -3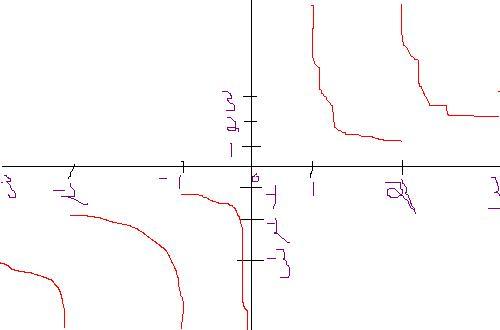
13 Answers
virang1 Jhaveri
·2009-07-17 01:05:49
virang1 Jhaveri
·2009-07-17 04:39:49
is my graph rite sir
The hyperbola in the solution mean a part of it
Mani Pal Singh
·2009-07-17 22:14:26
na ji na
study the definition of {x} again and den try the question!
°ღ•๓ÑÏ…Î
·2009-07-17 22:37:48
rite side is right ..left mein gadbad hai :)
take
-1.2
so [x]=-2 ....n {x}=.8............
n so on
eureka123
·2009-10-05 01:41:49
looks like everyone forgot abt this one.....
just completing it...
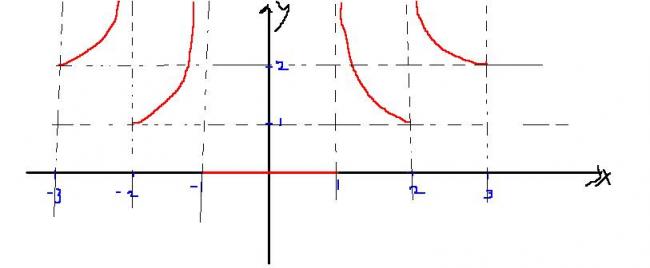
the red lines indicate graph..the black ones are just grids
Lokesh Verma
·2009-10-05 01:59:26
no eureka..
you have done a fantastic job.. but you seem to have missed something on the left side..
what is it?
Lokesh Verma
·2009-10-05 02:01:51
Virang;s graph was very good.. he just overlooked a small thing as pointed out by mrunal..
$ourav @@@ -- WILL Never give
·2009-10-05 04:02:31
eureka,den make corrections and post d graph again