i think there should be a small correction, asish :
the graph touches the x-axis when secx = 1
Q
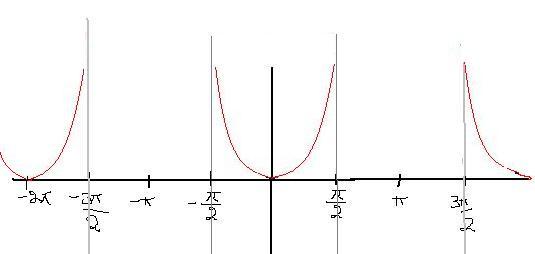
Draw the graph of log(sec x ) providing all the analyzes and do it as a question is meant to be done (from basics)
range of secx is (-∞,1]U[1,∞)
But for log(secx), secx > 0
So, domain = ((2n-1)Î /2,(2n+1)Î /2)
f(x) = log(secx)
f'(x) = tanx
f''(x) = sec2x >0
further as secx > 0 so, log(secx)>0
further y=log(secx) is even function
So symmetrical abt y-axis.
i think there should be a small correction, asish :
the graph touches the x-axis when secx = 1