39if this is the case, it is sin(x+y)=a
17 Answers
21SLOPE OF THE GRAF : -1 thruout......
intercepts change..........
as
2nÎ + sin-1a
or
(2n+1)Î - sin-1a
provided -1<=a>=1
62btw the graph was wrong :)
ashish posted this scrap to me to tell me :)
1wow!! this graph thread is looking so beautiful !! all pink pink...
btw ... nice questions :)
106x+y = 2nÎ + sin-1a
or
(2n+1)Î - sin-1a
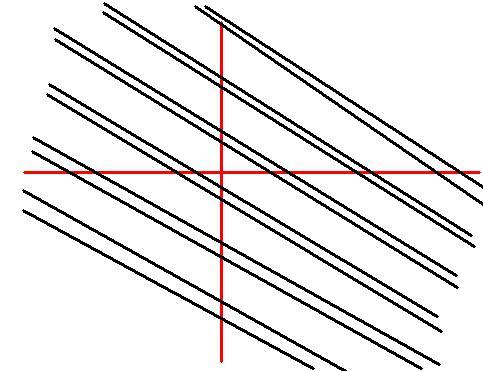
So, it will be infinite no. of straight lines of two types:
TYPE 1:
slope = -1
parallel to line of y-intercept = sin-1a at regular y-intercepts of 2Î
TYPE 2:
slope = -1
parallel to line of y-intercept = Î -sin-1a at regular y-intercepts of 2Î
62because this one is a sitter for a graph of the day question.. lets do some more varaitions.
sinx. cosy + cosx siny = a
draw the graph
106general.....
sinxcosx=a
==>sin2x = 2a
So, -1/2≤a≤1/2 then only it is possible.
Then x = nÎ /2 + (-1)nsin-1a/2
21[11] [11] [11] [11] [11] [11] [11] [11] [11] [11] [11] [11] [11] [11]
that means 2sinxcosx = 2;
sin(2x) = 2;
thats not possible
null graf???????
62How about
sin3x cosx + cos3x sinx =2
and
sin3x cosx + cos3x sinx =a
106there is no solution according to me...
Bhaiyya what am i getting??
sinxcosx=1
==>2sinxcosx=2
==>sin2x=2 which is impossible so no solution...
kya yeh sahi hai?