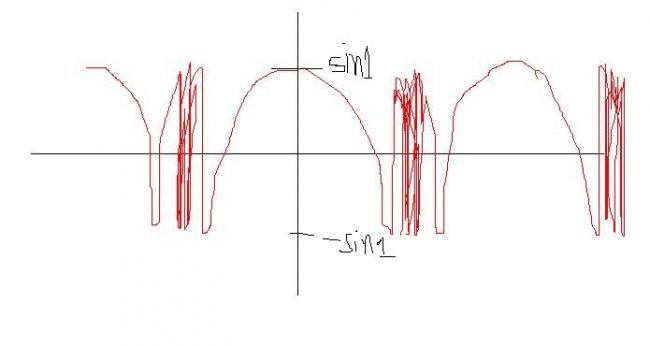
range is but obviously -1 to 1 but i think that domain is R-n∩/2
15 Answers
phew.. yes.
but this will be too tough for me too.. I will tone down the question a bit :)
for y=sin(cos(tan x)))
proceeding in very orthodox manner i guess
the dom is r-(nπ/2) an
the range is (-sin1,sin1)
then calculating the nature of the graph
1)pts of discontinuty n x Î /2 as tan goes undef. there
2)pt. of maxima x=0 as cos 0=1
3)similarly pt. of minima
4)behavoiur 0 <x<Ï€/2
tanx increases
cos(tanx) decreases
sin(cos(tan x))) increases
5) behavoiur π/2<x<π
tanx increases
cos(tanx) decreases
sin(cos(tan x))) decreases
this is for sin(tanx)
doms : R - (n+.5)Î
functn is increasing on : tan-1(-Î /2)<x<tan-1(Î /2)
functn is decreasing on : tan-1(Î /2)<x<tan-1(3Î /2)
at x=nÎ y = 0;
pases thru origin
range : [-1,1](obvoiusly)
the inc.-dec. pattern folows da same order for multiples....
basically da idea is 4 jus 1 full circle!!!
is it rite??
tapan's dom and range are rite....
as x comes close to π/2...it will oscillate very close....discontinuity at π/2....the pattern will continue....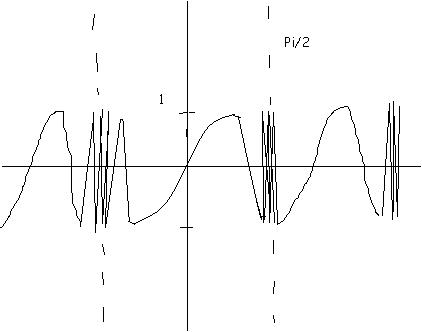
not that goodlooking.....
@abhishek.. between 0 to pi/2
tan x goes from 0 to infinity.
so sin(tanx) goes from 0 to 1 back to -1 and so on a huge no fo times..