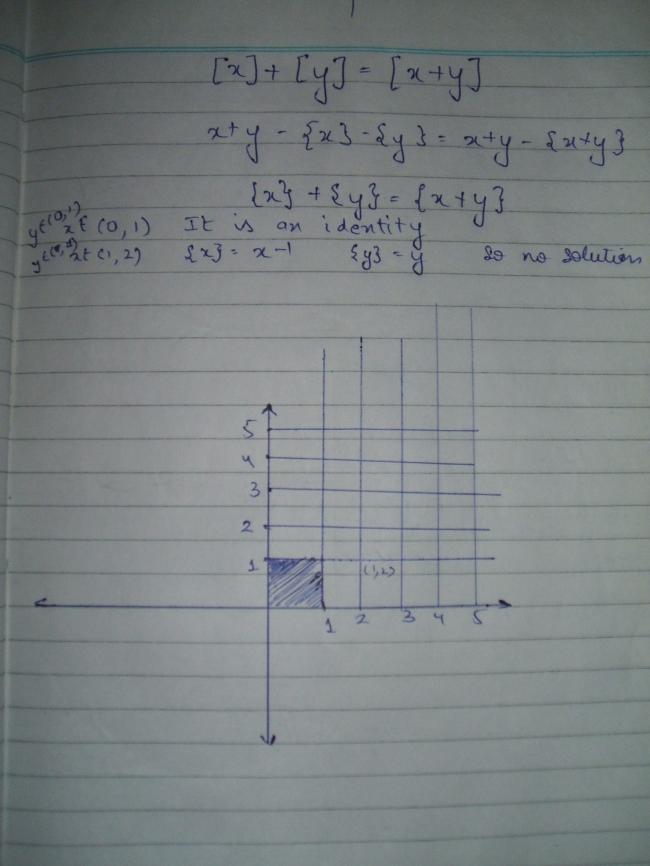
Can the graph be chunks of area since it is not a st. line
8 Answers
tapanmast Vora
·2009-03-20 02:25:40
hmmm.....
AL INTEGERS,
samr as {x} + {y} = {x+y}
so {x} + {y} < 1 always.......... SO ALL CASES wer both {x} & {y} are gr8er 0.5 and many more shall be forgtten forever
symetric abt both the axes!!! i.e abt ORIGIN
Asish Mahapatra
·2009-03-20 20:57:12
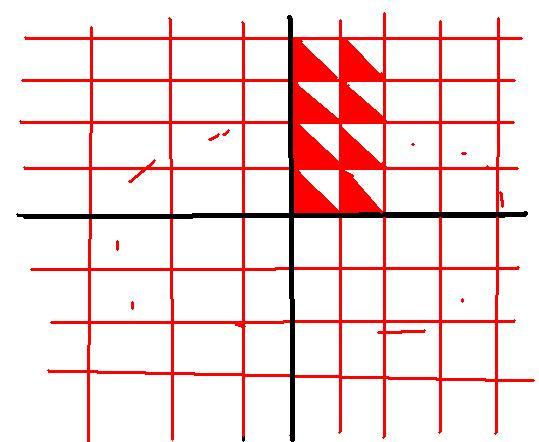
the graph is copy pasted after we solve it in the section x belongs to [0,1).
In [0,1) [x]=0 and x={x}
So... [y] = [{x} + [y] + {y}]
==> [y] = [y] + [{x} + {y}]
==> [{x}+{y}] = 0
==> {x} + {y} belongs to [0,1)
virang1 Jhaveri
·2009-03-20 23:30:17
No.
IS it like this 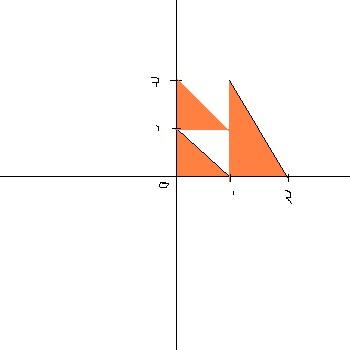
The Triangle have the same shape as you go up the graph