1thank u
21 Answers
62There is nothing wrong so far except that this seems to be a dead end to me ! :P
I mean i dont see how to move ahead from ur step..
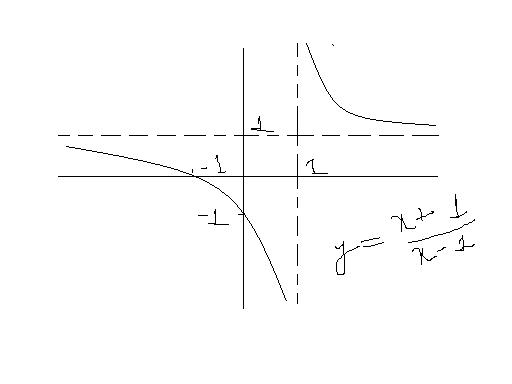
1ok so the graph of the above function is a rectangular hyperbola which is shifted 1 unit to the right and 1 unit upwards from the origin
62@Amritansh
Hint:
if we have f(x) 's graph then how do we draw the graph of f(x+a) ???
1can sum1 explain me how to approach and draw the graph of the given function after i think of the hyperbola xy = 1
6m ploting for d modified part of mine...i got d numertaor bt hw to go wid d denominator dats wat my doubt was..........
1just think of the rectangular hyperbola xy=1 i.e. y=1/x, now to get the graph of y=1+1/x, shift the graph by 1 units...n u hv drawn only half of d graph...dere should be another arm
correct me if i m wrong......
.after dis hw to approach??
62we are only looking at the points where the function's deno becomes zero...
and then find the limits of the function as x goes close to that point and also close to infinity...
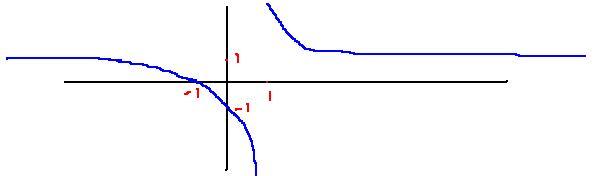
The graph closely follows 1/x as shown by karna in #6
6i can rite the expression for dis as (1+1/x)/(1-1/x)
i got te graph for the numerator
wat abt the denominator??pls help
1we can write.......
\frac{x-1 +2}{x-1}
1+\frac{2}{x-1}
that is a rectangular hyperbola displaced 1 unit towards riht and then elevated to 1 unit above x axis
24y=1 +2/x-1
at x=1 ,y→∞
domain=R~{1}
Range=R
neither even nor odd..
not periodic
X intercept => y=0 =>x=-1
Y intercept =>x=0 =>y=-1
y'=-2/(x-1)2 <0 for all x
y'=∞ at x=1
y"=4/(x-1)3
y"<0 for x<1 => convex dec
y">0 for x>1 => concave dec
x=1 is assymptote
as x→-∞ ,y→1
as x→+∞,y→1
