bhaiyya is {} fractional part??
No credits without explanation of this one..
(x2+y2-2)(xy-1)<0
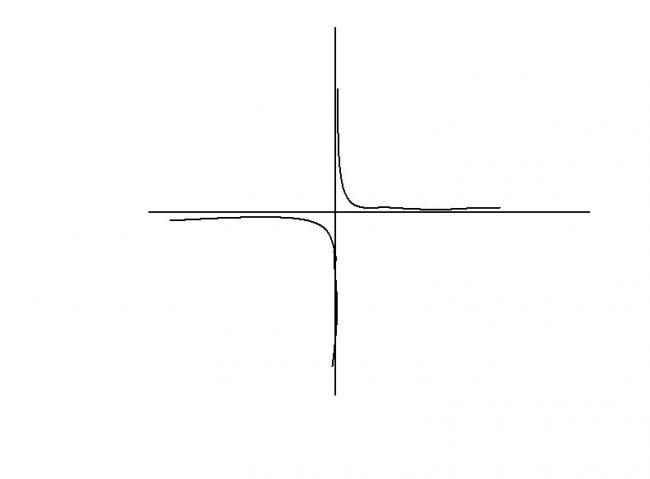
draw the graph!
-
UP 0 DOWN 0 0 14

14 Answers
from the given equation
x2+y2-2<0
x2+y2<2
y<√2-x2 or -√2-x2
from this graph is below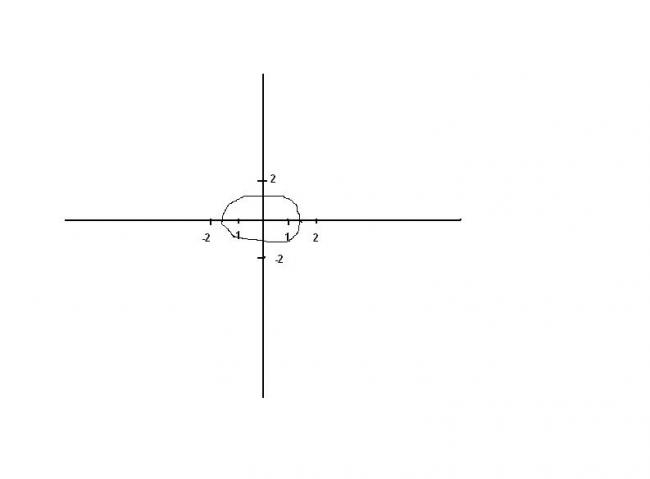
@ amit.. that eqn can be greater than 0 or less than 0 it will never be always less than 0 .. consider when xy = 0.5 then xy-1 <0 so the eqn u have considered has to be > 0 for the inequality..
so joint graph is given
here the graph of y=1/x and y<√2-x2 or -√2-x2 touch each other at two points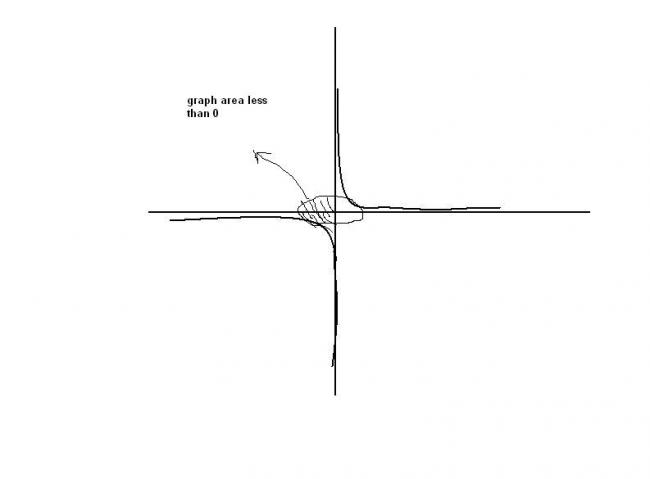
CASE I when xy-1 > 0
then x2 + y2 - 2 <0
take a complex no. z = x+iy.. then lzl2-2<0
==> lzl<√2
now. xy-1>0
let z=rcosθ + risinθ
==> x=rcosθ and y=rsinθ
==> r2.sin2θ > 2
==> sin2θmax = 1 ==> r2min>2
==> lzlmin>√2
So. no solution if xy-1>0
CASE II when xy-1<0
then w2+y2-2>0
==> lzl>√2 ==> lzlmin = √2+
now.. xy-1<0
==> r2sin2θ < 2
when sin2θ = 1 lzl<√2 so no solution..
when sin2θ < 0 then all values of lzl has solution
as sin2θ value decreases from 1 to 0 lzl increases from √2 to ∞
So. the solution is:
when sin2θ<0 then lzl>√2
and when sin2θ>0 then lzl value decreases from ∞ to √2+ as 2θ increases from [0,π/2) and reverse order when 2θ increases from (π/2, π]
case1
x2+y2-2>0
and xy-1<0
simultaneously
so
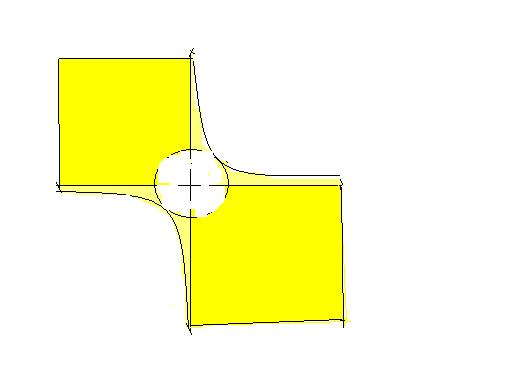
outside the circle and inside the hyperbola
case2
x2+y2-2<0
xy-1>0
so inside the circle and outside the hyperbola
which isnt possible so case 1 suffices