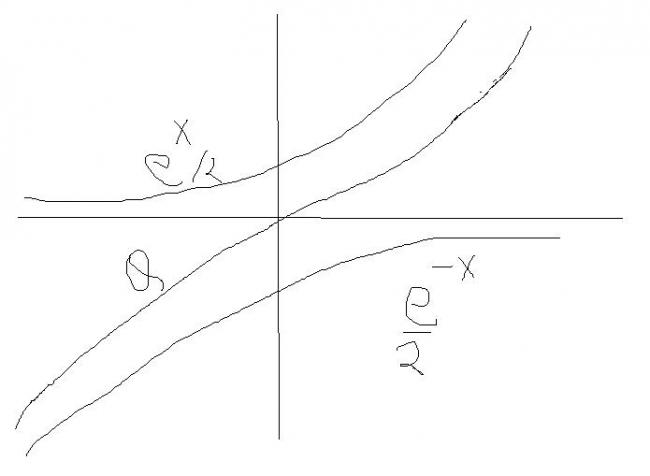
106y=(ex+e-x)/2 is always positive..... and so its second derivative is always positive..... its first derivative is (ex-e-x)/2 which is positive when x>0 and negative when x<0 ... at x=0, y=1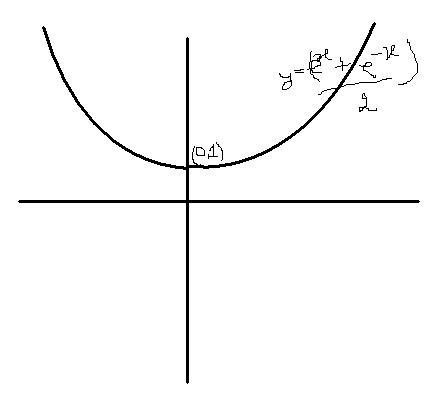
draw the graph of
y = (ex + e-x)/2
y = (ex - e-x)/2
and y= (ex - e-x)/ (ex + e-x)
-
UP 0 DOWN 0 0 16
16 Answers
106106y=(ex-e-x)/2
dy/dx = (ex+e-x)/2 which is always positive
d2y/dx2=(ex-e-x)/2 which is positive when x>0 and negative when x<0.
at x=0,y=0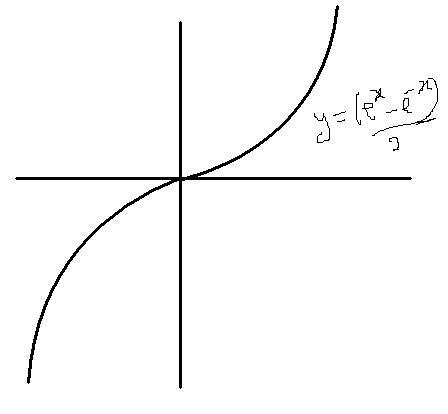
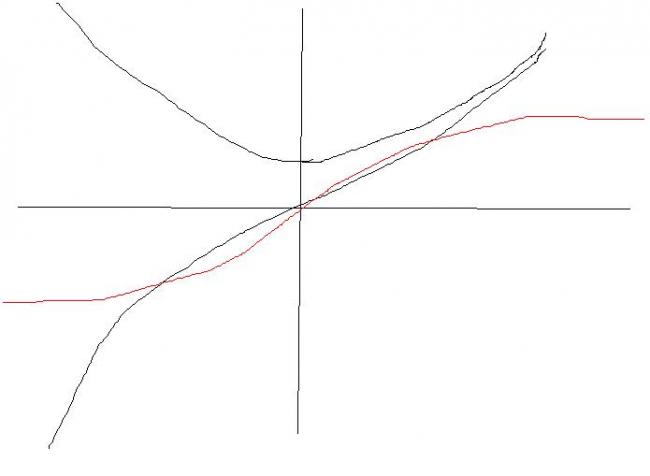
33Simple ones.. just addition subtraction and division of graphs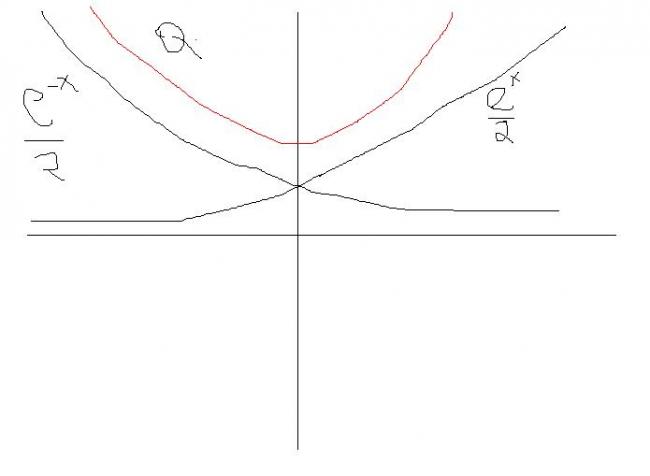
addition of graphs....
106y=(ex - e-x)/ (ex + e-x)
dy/dx = 4/(ex+e-x)2 which is >0
d2y/dx2 = -8(ex-e-x)/(ex+e-x) which is >0 when x<0 and <0 when x>0
At x=0,y=0
But as x increases or decreases...... ex+e-x becomes very large..... hence at large values of x, slope becomes almost zero...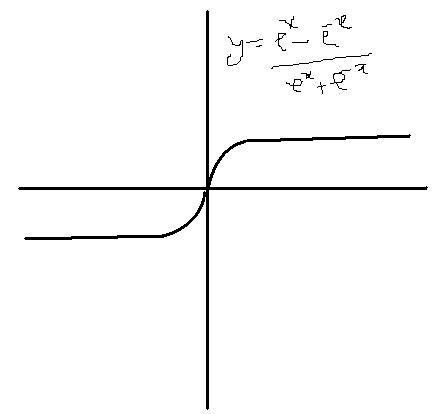
lines after large valus of x are almost straight
106gr8 priyam and mee same graphs although i like his method better [3]
21hey akand the xpression u hav written is 4 e^ix.... DUDE!!!
and obviously if e^x = cosx
then it wud never inc 1 is that possible [7]
106nishant bhiayya, are priyam's and my graphs for y=(ex-e-x)/2 wrong??
62no they are not...
I just missed them among the numerous graphs ;)