1bhiya is dis right?
23 Answers
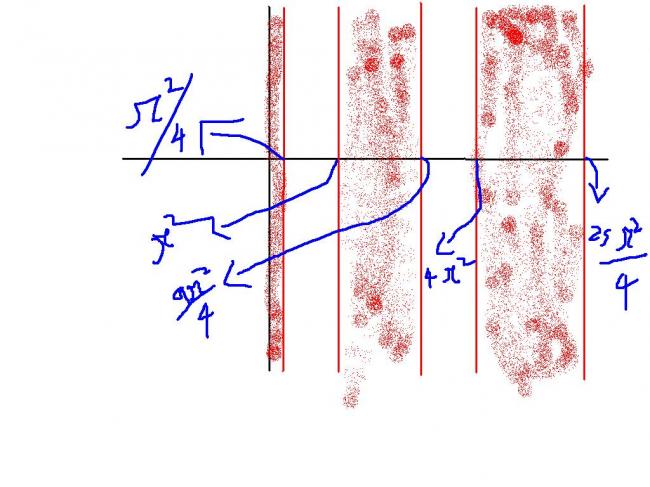
12n\pi <2\sqrt{x}<(2n+1)\pi
n\pi <\sqrt{x}<\frac{(2n+1)\pi }{2}
squaring
n^{2}\pi^{2} <x<\frac{(2n+1)^{2}\pi^{2} }{4}
region
keeps on increasing
will
post graph quickly
21Sir, I totally Agree wid MAK's SOLUTION,
but as a matter of 1st sight idea, the area wer sin n cos both r -ve will b shaded totally!!
Is dat crrct way of thinkin......
and weat MAK told abt other cases is quiote precise
62yes mani..
see MAK's work... It is a bit more general and better than I had expected :)
21Sir : ISnt this rite :
pura ka pura 3rd QUADRANT excpet Î and 3Î /2....... seeing frm the fact dat sin2x<|sinx|
as |sinx| < 1
1ok nishnt bhaiya can u give IIT-jee problems on chemistry , not seen many problems of iit on chem..
21not useful : [2]
0.5* sin(2√x)*(1 + sin√x + cos √x + 0.5* sin(2√x)) > 0
easier wud b :
2 cases :
1) both brackets > 0
2) both brackets < 0
as |sinx| > sin2x excpet wen sinx = 1,0,-1
MATLAB pura ka pura 3rd QUADRANT excpet Î and 3Î /2....... as -ve * -ve = +ve
62@amit..
yeah that is why i put it back :D
Three boys being punished in class... stand with your hands up ;)
1ohh nishant bhaiya remove that graph, its so funny and even wrong, so i had deleted it[17]
1yeah... somewhere 2 yrs back...!!! :D
well, i edited it... now have a luk... :)
62
Amit where did you get this from ;)
this is a nice looking one..
3 men with hands stretched upwards ;)
like we used to be punished in the class :D
21OH YAH!!!!!!
I did pretty much this but then cancelled it!!! [2] [17]
Nice one MAK
1=> sin√x.cos√x.(1+sin√x + cos√x + sin√x.cos√x) > 0
=> sin2√x.(1+sin√x + cos√x + sin√x.cos√x) > 0 =>
sin2√x.(1+sin√x).(1+cos√x) > 0
=> sin2√x > 0 ....... since the other two are always greater than zero)
solving dis gives nΠ< √x < (2n+1)Π/2 ..... n>0
also d solution set would be excluding d points where sin√x and cos√x = -1...
let me know if i'm wrong anywhere...!!!