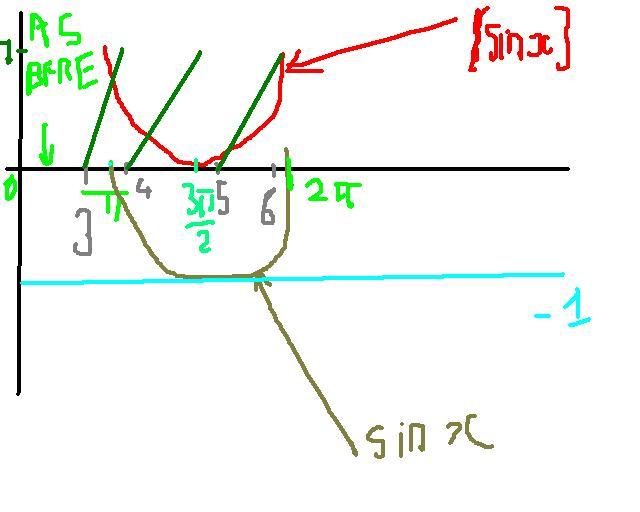
yep small error in drawin...
{sin x} = {x}
I dont know the solution.. but this one looks intimidating for the first time.. :P
Lets see if we can figure out something useful here.
-
UP 0 DOWN 0 0 17

17 Answers
yes celestine.. you are right.. there iwll be no general solution..
@iitimcomin in ur post #6... the graph of {sinx} cant intersect graph of {x} before x=Î /2
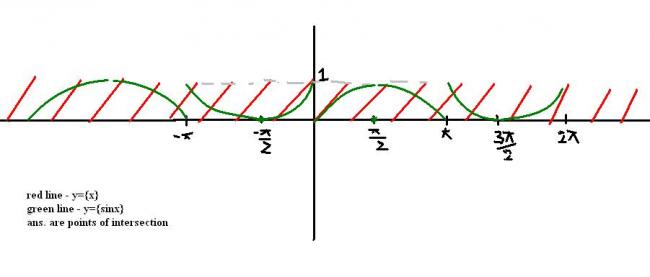
u can draw the remaining graph by periodicity..
Note:
The solution in x ε [0,Π/2) is x=0
sorry in graph 2 the green line dosnt meet with the red line in the right part .... hav butter fingers [3] .........red part is near 2 pi and green part is near 6 ... and moreover tey dont reach y=1 as i said before!!!
for {x} at y=1 .. its all holes [3] ...... they dont go till 1 not depicted clearly ............
same with {sinx} .....
@mathie... "its basicaaly drawing x=sinx and x=sinx±1" i dont think so... consider x ε [2Π,5Π/2). here
[x] can be 6 or 7
but [sinx] = 0
So, graph will be x-6 = sinx
or x-7=sinx
sorry all the green lines shud have same slopes but in my graph its not all dat accurate,,,,
the intersection points will be soln...... there will be ∞ soln. i think ....... ulll hav to spify a range!!!!!!i think...............
correct me if im rong....still a beginner[2]
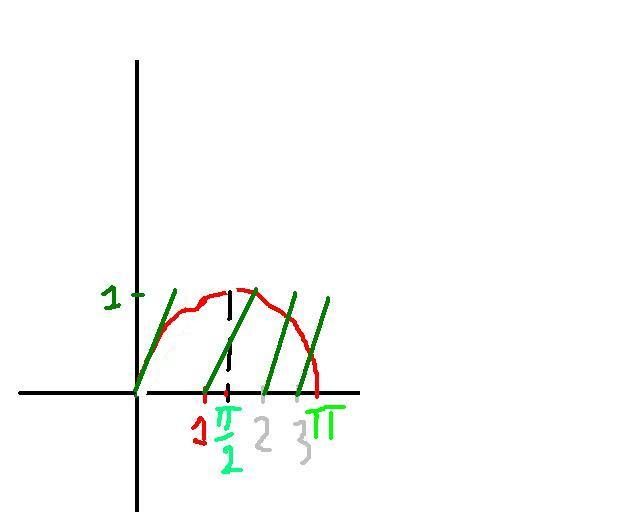
i think first part will luk like this ..... sin anyway is below 1 so its part till 1 will be same as sinx curve and after that at pi/2.... it will drop to 0 !!!!!![discontinuity] ...............
i have yaken that x belongs to [o,Î /2] and [-Î /2,0], but i think now it can be generalised.
its basicaaly drawing x=sinx and x=sinx±I (I is an integer)
bhaiyan, am i right or wrong?
now taking other general case when sinx≤0
now x belongs to [-Î /2,0] [sinx]=-1 thorughout
subcase 1: [x]= -1
x=sinx
subcase 2: [x] = -2
x= sinx -1
see the given question can be written as
x -[x]= sinx - [sinx]
lets take the case where sinx≥0 i.e x belongs to [0,Π/2]
in this intrval, [sinx]=0 but [x] can be 0 or 1
sub case1: [x]=0
now the graph is simply x=sinx
sub case 2: [x]=1
now the graph is simply x=sinx+1