thanx 4 the link, bhaiya...
this question was dere in fiitjee open test
4 identical balls of radius R and mass m are lying in a gravity free space. The balls are in contact and their centres are forming vertices of a square of side 2R in horizontal plane. One identical ball travelling vertically wid speed v hits the 4 balls symmetrically.. The collision is perfectly elastic.
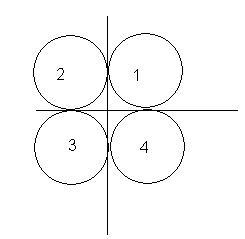
Q1. wat is the speed of ball 1 after collision??
Q2. What is the speed of the ball which was initially travelling wid v?
Q3. Unit vector in dir of motion of ball 2 is wat?
-
UP 0 DOWN 0 0 4

4 Answers
there was a similar question of the day which i thought was a unique question..
where did u get this from?
http://targetiit.com/iit_jee_forum/posts/19th_november_2008_587.html
Consider the system of 4 balls to be acting on the COM.
Momentum conservation equation along z-axis:---
mv = 4m*v1 - m*v2 ---- (i)
As, the travelling ball will return by the same path due to symmmetry.
e = velocity of separation/velocity of approach
1 = (v1+v2)/v
v = v1+v2 ---- (ii)
Solving 1 & 2
we get,
v2 = 3v/5;
Now apply energy conservation equation before and after collision, as it is elastic collision
energy will be conserved.
consider, speed of 4 similar balls = v3
0.5mv^2 = 0.5*4m*(v3)^2 + 0.5 *m*((3/5)v)^2
m*(16/25)*v^2 = 4m*(v3)^2
v3 = 2v/5;