1lets see after getting the fbd rest is just kinematics!!
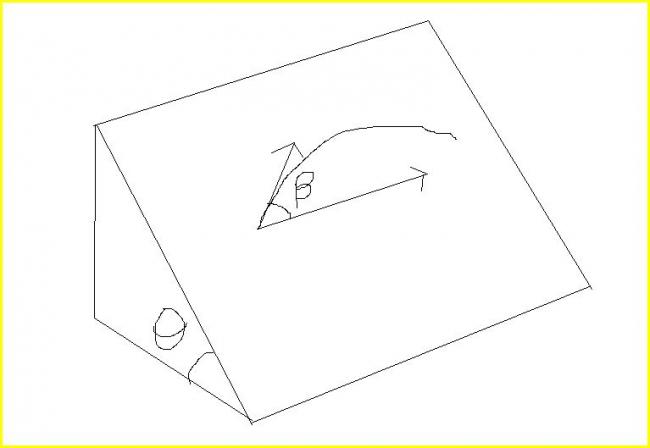
a particle of mass m is give a certain velocity along a plane which is at angle θ to the horizontal.
the velocit given is at a angle of β to the horizontal and the coefficitnet of friction is μ>tanθ
hence as the particle stops find the direction of its velocity just before stopping .
-
UP 0 DOWN 0 2 26
26 Answers
9but rohan on what basis are u saying its downward for any other angle ?????
1my solution ultimately leads to your equation celestine but one step you missed as i shall show
see that just before stopping , V->0
Hence V1^2 +V2^2 ->0
thus
Vx->0 and Vy->0
hence v1/v2=d(v1)/d(v2) (By L hospital's rule) = (md(v1)/dt)/(md(v2)/dt)=F1/F2
where F1 and F2 are the forces on the object in the respective directions
but v1/v2=dy/dx=tana
hence writing the differential equations and solving for a
we get a as pi/2 or -(pi/2)
hence the body either moves in the upward direction or in the downward direction before stopping
uppward- when we give initial velocity along y only
downward - at any other angle ..
9let v be at angle @ with downward vertical jus b4 stopping
let F be friction
mvcos@ = (Fcos@ -mgsinθ)dt
mvsin@=Fsin@dt
if sin@≠0
Fdt=mv
putting in first eq
we get mgsinθdt =0 implying dt=0 which is wrong !!
1no celestine not necessarily
for example let the body be thrown straight down .Before stopping acceleration = gsinθ-μgcosθ
but after stopping 0
9rohan in this case net force is 0
i wasnt telling in general
9course of nature is continuous we know net force after stopping is 0 and hence friction acts upwards !!!!
1and just before stopping friction may not balance mgsintheta upwards
it may act in a definite direction depending on velocity
before stopping let vx=a vy=b then a and b both are very less how can you say that frction direction is opposite to mgsintheta!!!!!
1hey celestine ; how can you say that net force is zero when it stops !!!!
for example take a spring when it stops is the net force zero ???
1
vy=gsinθ - μgcosθ
vx=μgcosθ
vx=0 when t1=(v0cosβ)/(μgcosθ)
vy=0 when t2=(v0sinβ)/(gsinθ-μgcosθ)
if t1>t2 - velocity before it stops is down the plane
not able to come to a definite conclusion
9ok by logic its got to be downwards
see after stopping net force is 0
jus b4 stopping friction balances mgsinθ down the plane approximately
ie Friction up plane this is possible when v down plane
9oops totally forgot abt this Q
k im trying
u may expect a sol in 2-3 days :)
9ok i ll give a greater treatment to this after april26
( by logic its easy to say)
1celestine what if beta is negative?
and how can you say that horizontal belocity is reduced more?
when angle with horizontal =α then force opposing horizontal acceleration = -Fcosα
and for the vertical = -mgsinθ-Fsinα
you cant say that the quantity above will always be greater than that ..
infact after some time when α becomes zero then there is no frictional force donwards...
and maybe then horizontal and vertical velocities become zero at the same time ...
9friction always opp velocity and also gravity acts down
so vertical vel is reduced more than hor vel so wen vertical vel is 0 , there is some hor vel now again hor vel is reduced but vertical vel inc initially and then somewhat opposed in later stages
continues till hor vel 0 and then only vertical vel down remains
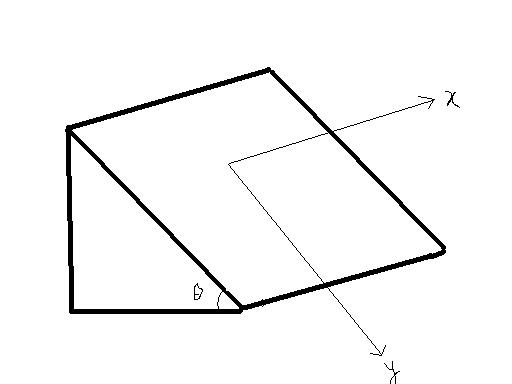
1its the same figure as the simple yet good one
instead of throwing horizontally it is thrown along the plane at an angle β to the horizontal
