11x = u2cosθ/g
z= u2(2sinθ - 1)/2g
is it rite?
A machine gun of mass M/4 is mounted on a plank of mass 3M/4. The barrel of the gun is inclined at an angle of θ with the horizontal. The plank is moving on a smooth horizontal surface in x-y plane of a coordinate system along positive y axis with a speed V. A bullet is fired with the speed u relative to the plank in x-z plane. Find the coordinates of the bullet with respect to the point of projection, which is fixed in the ground reference frame, at t=u/g (assuming the bullet does not fall back to the ground till this time). The positive Z axis is vertically upwards!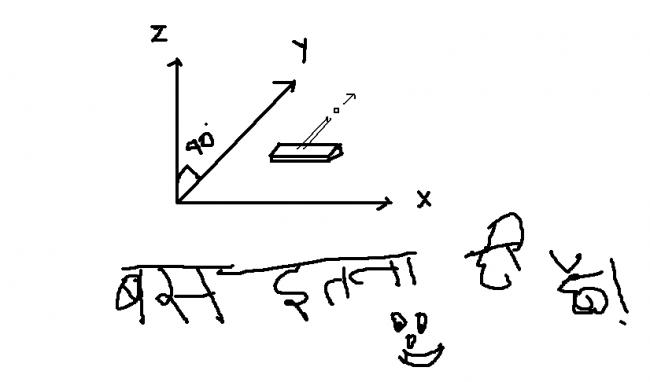
TAKE THE MASS OF THE BULLET TO BE m
-
UP 0 DOWN 0 0 16
16 Answers
6no yaar this is not the answer!
there should be mass term too included!
this is not the answer!
3hey then the mass of bullet shud be given !! if we have to apply conservation of linear p, they shud give the mass of the fired bullet !!
3if we are simply to apply kinematics, then i think mass will not be involved newhr...
6no no you have to get the mass in the answer!
this is the complete question now i have rechecked! sorry could not continue th link i am leaving for gym!
24body shoddy bana raha hai kya???????[3][3]impress everyone in IIT[9][9]
6no no eureka nothing like this! its all a part of daily routine! so i have to go for two hours, one hr in morning and one in evening! well the most important of all
KOI MUJHE ISKA SOLUTION DE DO!!!!!!!!!!!!!!
for the students who do not understand hindi,
RELP I NEED THE SOLUTION!!!!!!!!!!
1well let the velocity of the combined system of machine gun and plank be v1 along negative x axis and v2 along y axis after the bullet is unleashed
then as the bullet was launched at a speed u w.r.t the gun the velocity of the bullet w.r.t the gun along y axis must be zero
(AS the gun is atr an uniform angle theta in x z plane
)
let the actual velocity of the gun be v3 with an angle of β to the x,z plane with x
Further as the bullet is launched perpendicular to the motion of the plank the relative velolcity along y must be zero
Mv=(M-m)v2+mvx
but vx=v2
thus we get v2=v and velocity of the bullet along y= v
further consercing momentum in the x-z plane
(M-m)v1=mv3cosβ
as the velocity of the bullet w.r.t plank is u ,its horizontal and vertical components must be ucos and usin theta
thuis
v3cosβ+v1=ucosθ
v3sinβ=usinθ
solving we get v3 cosβ and v3sinβ as the following
ucosθ-(mucosθ/M)
and usinθ
hence y coordinate=vt=vu/g
z coordinate= vsinβt-1/2gt2=u2/g(sinθ-1/2)
x coordinate=v3cosβt=u2cosθ/g(1-(m/M))
