33cosα=1/2
[7]
A block slides down a smooth track of height 50cm and then enters into a loop of radius 20cm from which a symmetrical section of 2α has been removed.Find angle α such that after leaving the circle at A and flying through air,the block will reach point B?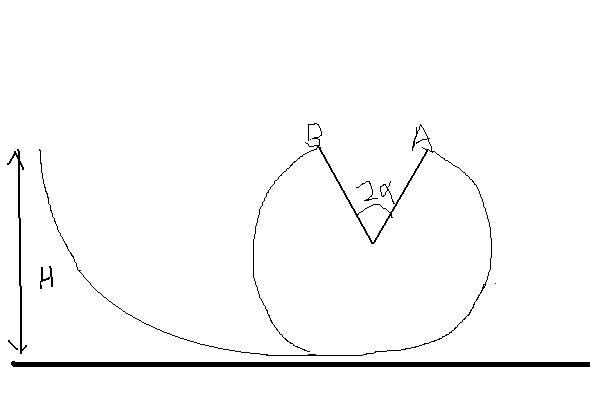
-
UP 0 DOWN 0 0 7
7 Answers
33By writing energy conservation between initial ht and A find speed at A... direction will be tangential.. at A after that a projectile solve it like a projectile and write condition o reach B from that u will get α..
Try this theres nothing conceptual.. all calculations and i hate doing that :P
33Only in short i am giving..
velocity at A is tangential to circle.. so velocity there will make an angle α with the horizontal..
now its projectile with u at an angle α and range should be 2Rsinα (distance b/w A and B)
from range eqn get a relation between α and u
u=(10R/cosα)1/2
now energy conservation b/w initial pt and A
mgH=mgR(1+cosα)+1/2mu2
put the value of u ..
u=(10R/cosα)1/2
and solve to get α=0,cos-11/2
notice significance of α=0 in the answer
cHeErs.. :)
33For projectile motion b/w A and B..
Superposition method gives the relation easily..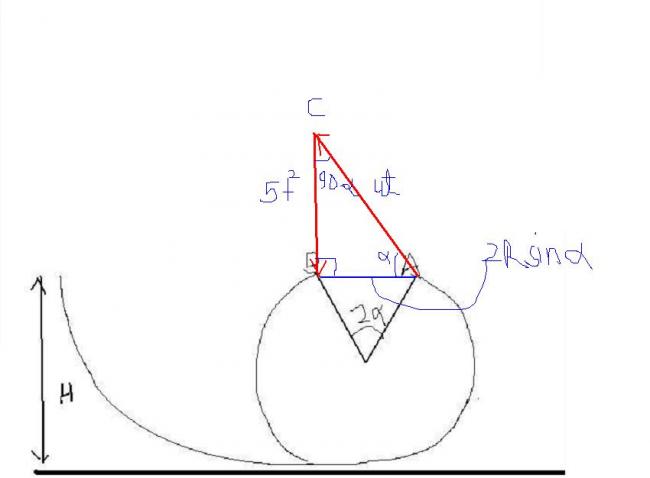
Now in ΔABC.. applying sin law..
ut=2Rsinα/cosα=5t2/sinα..
eliminating t gives the relation u=(10R/cosα)1/2 which i used above..