HINT : apply one torque eqn and one force eqn[1]
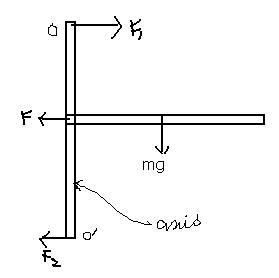
Q. A horizontally oriented uniform rod AB of mass m=1.4 kg and length lo = 100 cm rotates freely about a stationary vertical axis OO' passing through its end A. the point A is located at the middle of the axis OO' whose length is equal to l=55cm. At what ang. velocity of the rod the horizontal component of the force acting on the lower end of the axis OO' is equal to zero? What is in this case the horizontal component of the force acting on the upper end of the axis?
-
UP 0 DOWN 0 0 15

15 Answers
eureka can u tell me where the force will act?. I mean where should we consider the force to act.
If we consider the entire system, mg will act on the horizontal rod. Where will the hori. force act? (on COM of axis or on top)
see in hte question itself we are given that 2 horz forces act..one at the top od OO' and othere at botton of OO'
assume them to be F1 and F2....
now can u finish it ???
but wont a force act at the COM of the axis (though it is not given but doesnt the force on a body act at its centre of mass?)
quite an ambiguous question .......cant exactly say where the rxn forces are acting ..... but lukin at the 55cm stuff i took it to be the ends of the axis ..
thats wat im saying.. the force acting on a body (here axis) acts at the COM. (the midpt.) So thats y i gave that F
note: in ur first eqxn the L on RHS and LHS are not same .........
these eqxns i rote earlier ...
ashish post 8 is partly correct
ur concept is right
now u need to add verticle forces at O and O' to balance mg
eureka
at A only horizontal force can act
vertical force to act implies friction
is there friction here ?
Celestine, at end A there will be vertical forces also, in general. You don't know how it has been connected to the axle; it might have been welded as well.
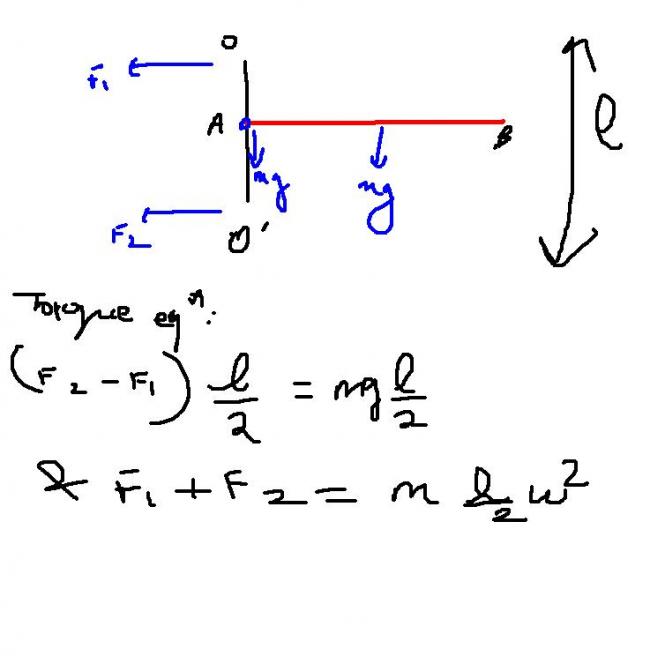
The problem can be easily tackled if we take our system as the rod + the axis. Then the reaction at A becomes an internal force. Take the reference frame that rotates at the same rate as the rod. In this reference frame our system is in rotational equilibrium. So the net torque should be zero about any point.
Taking the moments about the upper point (point O in #8), we see that the torque due to gravity must be balanced by the torque of the (pseudo) centrifugal one (since there is no horizontal reaction at the bottom). This gives
mg\dfrac{\ell_0}{2}=m\omega^2\dfrac{\ell_0}{2}\cdot \dfrac{\ell}{2}
from where we get the required angular velocity as
\omega =\sqrt{\dfrac{2g}{\ell}}
In this case (coming back to the inertial frame) the centripetal force required by the rod to rotate in supplied by the horizontal reaction at the top, and hence
F_{h,\,\mathrm{top}}=m\omega^2\dfrac{\ell_0}{2}=mg\dfrac{\ell_0}{\ell}