 33
33With respect to the center of larger cylinder...
Initial ang momentum is I2ω0+m1V1d sin(00)...........
v is velocity with which smaller cylinder is brought closer and d is distance of COM of smaller cylinder at any time... (Don't think me a fool) but as the angle is 00 between distance vector and velocity vector therefore that term becomes zero...
finally let F be frictional impulse so torque due to it about center of larger cylinder(where our observer is from the start of the question :))
Ï„=FR2-FR2 which comes out to be zero....
so as there is no external impulse about center of larger cylinder so angular momentum will conserved about it(the resting place of our observer from the start of this very long explanation..)
therefore..
I2ω0+m1V1d sin(00)=I1ω1+m1vc(R1+R2)sin(θ)+I2ω2.........(ii)
where vc is velocity of center of mass of smaller cylinder (which here is zero) and (suppose initially ω0 was clockwise) ω1 is anti clock wise and ω2 be clock wise...
also as there is case of pure rolling at the point of contact therefore..
ω2R2=ω1R1............(iii)
Putting value of ω2 from equation (iii) in equation(ii) we get the answer..
I2ω0=I1ω1+I2ω2
I2ω0=I1ω1+I2ω1R1/R2
ω1=I2ω0/(I1+I2R1/R2)..............(answer)
 3
3ur answer is wrong. and the hint given in this question is to use angular impulse equation and also the angular momentum is not conserved as per the question.
 33
33Nahi.......
aisa nahi ho sakta.....
now i will leave studying physics... :(
and never solve a question of physics :(
 1
1i think d approach is .........
fR1 = I1α1
fR2 = I2α2
and
(ω0-α1t)R1 = α2tR2........
and
4th eq will be energy conservation........
 1
1i think i got sometrhing, but can u tell me which cyllinder is small ????????????
 1
1forget it,
i am considering 2nd cyllinder as small,
ω2=I1R1R2ω0/(I2R12+I1R22)
is it correct ?????
 3
3u r correct. but actually the first cylinder is the smaller cylinder due to its smaller radius.please post ur soln
 1
1i am considering the second cylinder to be smallest (:=0)
now friction force 'f' acts on both system,
f R1Δt = I1ω1
f R2Δt = I2(ω0-ω2)
after friction force stops acting,
ω1R1 = ω2R2
solve thest three equation's u will get the ans
(:-|)
 33
33Can any one tell why ang mom is not conserved...
read my xplanation above...
@ shankara
Does the smaller cylinder is constrained to remain in its line of approach or it can revolve around bigger one (alway in contact though)
[1]
that was a relay good question...
second case is also very interesting..
[1]
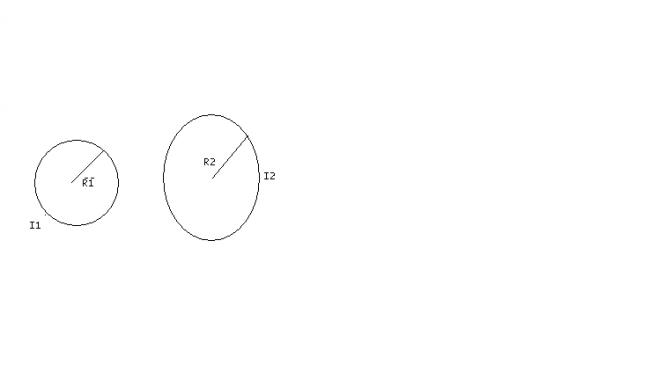 two cylinders having radii R1andR2respectivelyand rotational inertias I1and I2respectiveely are supported by axes perpendicular to the plane.The large cylinder is initilally rotating with angular velocity ω0The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two.Eventually,slipping ceasese andthe two cylinders rotate at constant rates in opposite direction.Find the final angular velocity ω2 of the small cylinder in terms of I1 ,I2,R1,R2 and ω0
two cylinders having radii R1andR2respectivelyand rotational inertias I1and I2respectiveely are supported by axes perpendicular to the plane.The large cylinder is initilally rotating with angular velocity ω0The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two.Eventually,slipping ceasese andthe two cylinders rotate at constant rates in opposite direction.Find the final angular velocity ω2 of the small cylinder in terms of I1 ,I2,R1,R2 and ω0