383pressure=HÏg
slant surface area=πR√(R2+H2)
force=(Ï€R√(R2+H2))*HÏg
Akash Anand Pressure is not constant throughout the slant surface area
Sayan Sinha Here, H is not the height below the fluid. It's the height of the cone.
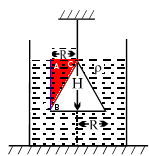
337We can calculate the area of the slant height using Ï€R√(R2+H2). Then, find out the area of the triangle ABC. Area= RH/2. Then, we multiply the area with the area of slant height = RH/2 * Ï€R√(R2+H2). Let this value be k. D=M/V. So, M=DV. Density is Ï and volume is k. We multiply them and get mass=Ïk. To find out the force, we multiply it using g. So, final answer=
Ï RH Ï€R√(R2+H2) g2
1161Well ..what would be the answer if the cone is replaced by a right circular cylinder of same base area and same height. This is a hint for this question.
Swarna Kamal Dhyawala the force exerted by liquid/ water will be equivalent to 2/3Ï€R2h(2/3*pi*R square*h) ie difference between volume of cylinder and cone337Sir,
Is this height the height of the cylinder? If yes, may I know at how much depth this cylinder is kept?
Also, do we have to find out how much force is exerted on the lateral surface of the cylinder or throughout the entire surface of the cylinder?
Thanx...
1Is total force=(2pi*R(∫(pi√(R2+H2)))*rho*g*∫H).....???
2305\dpi{150} \fn_cs \textit{Let us consider a small segment of radius r at a depth x below the surface}
\dpi{150} \fn_cs \frac{r}{x} = \frac{R}{H}\Rightarrow r = \frac{x\cdot R}{H}
\dpi{150} \fn_cs dA = 2\pi rdx = \frac{(2\pi Rx )dx}{H}
\dpi{150} \fn_cs \textit{Pressure by the fluid at a depth x = }x\rho g
\dpi{150} \fn_cs dF = P\cdot dA = \frac{2\pi R\rho gx^{2}dx}{H}
\dpi{150} \fn_cs F = \int \frac{2\pi R\rho gx^{2}dx}{H}
\dpi{150} \fn_cs F = \frac{2\pi H^{2}R\rho g}{3}
158B=pVg=TTR2pgH3=pressure on curved part+pressure on base
pressure on base=pgHTTR2
Pressure on curved surface=B-pressure on base=TTR2pgH3-pgHTTR2
