A boat moves relative to water with a velocity which is n(=2) times less than the river flow velocity. At what angle to the stream direction must the boat move to minimize drifting??
1here v_{r}>v_{br} so the boat can never reach the other end ...
more over if we consider minimum drifting :
drifting is given by x = ( vr - vbrsin θ)wvbrcos θ where w is width of river...
minimum drift i.e x = 0
→ ( vr - vbrsin θ)wvbrcos θ = 0
→ vr = vbrsin θ
→ sin θ = vr vbr
given is that \vec{v_{r}}=2\vec{v_{br}}
hence sin θ = 2 which is not possible
1vardaan are u sure of wat u wrote??[11].
cosec value -1/2......nayi trigo hai kya??[3]
106t = \frac{d}{vcos\theta}
x = drift =t*(2v-vsin\theta)
=\frac{dv(2-sin\theta)}{vcos\theta} = \frac{d(2-sin\theta)}{cos\theta}
=d(2sec\theta - tan\theta)
differentiating wrt \theta, we get
\frac{dx}{d\theta} = dsec\theta(2tan\theta-sec\theta)
which is zero when 2tan\theta=sec\theta\; \textup{or }sin\theta=\frac{1}{2}
this is also a point of minima.
Hence angle = 120° with river water direction.
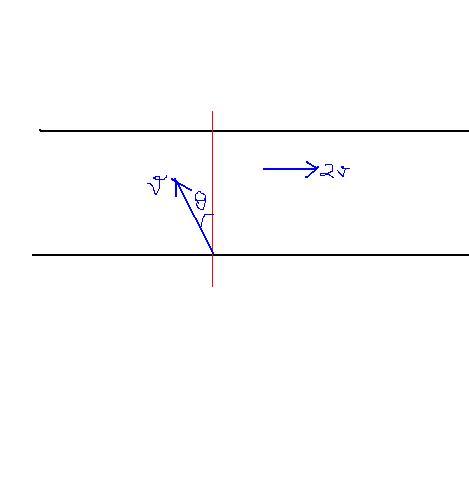
1ok i thnk i realised my mistake thnks to anand i was solving for zero drift which here is not possible since vr > vbr
i had to minimize " x " done wrongly in #2 :(
49@ashish and coolrocks:
thank you
yes 120° is the correct answer!!
[1][1]
so general answer is sin-1(1n)+Ï€2
!!
