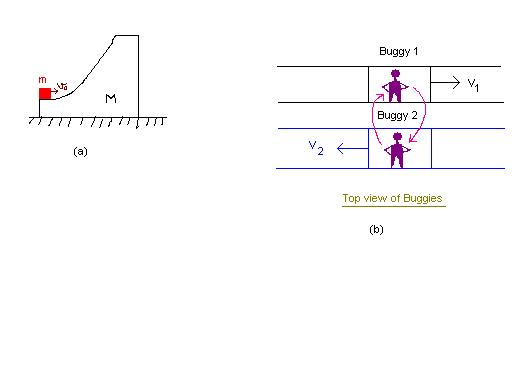
1(M+m)V=mV0.......................1
ALSO,
mgh=0.5[mV02-[m+M]V2].........2
substitute V from 1 in equation 2.this gives us h
FIGURE (a)
A smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from it's lowermost point with velocity V0 . What is the maximum height reached by the block ?
-
UP 0 DOWN 0 0 6
6 Answers
11i think the correct answer should be this
since force in horizontal direction is 0 the momentum of com of the system in x axis will always be be mv0
now considering the system the total kinetic and potential energy of the system will reman constant
so initially k.e.=mv2/2
and at highest point of mass m the vel of mass m will be 0 then the vel of mass M will be mv/M
thereofre k.e. =m2v2/2M
now chang ein k.e. = gain in gravitational enrgy of the system.... but the mass M doesnt rise
so if initally the com of mass M is at a hieght h2 and that of m1 at hieght h1
then com is at a hieght m1h1+m2h2/m1+m2 and after rising
m1h3+m2h2/m1+m2 and change in enrght will be m1h/m1+m2
so change in k.e. =m1h/m1+m2 and from this h is found out
nice conceptual question ...
1sorry one silly mistake
the chang ein k.e.=mgh
thereofre the answer comes out to be
h=v2(M-m)/2Mg
1@ kunl
If V is the common x- component of velocity then ur energy equation (2) is wrong
mgh=0.5[mV02-[m+M]V2].........2
because in applying the energy conservation we should take the net resultant velocity of the block that is the net resultant of the x- component and y- component velocity of block .
1@jasmine
do u know wat u r saying huh??
the equations i wrote are absolutely correct!U can ask anyone who knows "correct" way of learning physics and he will agree with the equations i wrote[1]