66At equilibrium, let x0 be the spring elongation so that 2mg = kx0.
If during the motion the body is at a position x (whose direction I choose to be downwards) from the equilibrium, then the total energy
-mgx +\dfrac{1}{2}mv^2 +\dfrac{1}{2}k\left(x_0+\dfrac{x}{2}\right)^2=\text{ constant}
Differentiating this equation w.r.t. time and using the fact that the velocity v = dxdt, we get finally the equation
\dfrac{\mathrm d^2x}{\mathrm dt^2}+\dfrac{k}{4m}\,x=0
from where we conclude that the angular frequency ω squared i.e. ω2 = k4m
The FBD of mass m during motion is mg - T = ma
The maximum amplitude Amax is determined by the fact that the tension in the thread becomes zero when the maximum acceleration is obtained. i.e. when a = ω2Amax. Hence we get g = ω2Amax i.e.
A_\mathrm{max} =\dfrac{4mg}{k}.
Accordingly, α = 4.
66
kaymant
·2010-03-30 10:59:10
@Asish, you are right. I actually balanced the pressures instead of the forces, which is wrong.
106Thanks a lot sir for those solutions.
Sir, for Q12. will option (a) be correct?
In Q10.
66
kaymant
·2010-03-29 13:24:37
@Grandmaster,
that equation you have written is not valid for all instants. You just took the initial instant and the instant when the block passes through the equilibrium. That x appearing in your equation is not a variable; its just the initial displacement.
1@kaymant sir,
imagine a in the beginning of the motion of the the block is slowly(i.e. v=0 at all pionts) pulled down for distance...the potential energy of the system is at this point is..
-mgx + 1/2k(x0+x/2)2
and kinetic energy at this point is zero....
when the block is released and it moves upward a distance x (when it reaches the datum level i.e.potential energy =0 and spring is stretched by x0) then total energy = 1/2kx02 + 1/2 mv2.......
so if we put total mechanical energy is constant at any time...then we get...
-mgx + 1/2k(x0+x/2)2=1/2kx02 + 1/2 mv2
which is differnt from your energy equation....[2][2].....sir please tell me if this approach is wrong and please pint out the error!!!!!
66
kaymant
·2010-03-29 04:42:35
Sorry Shreyan, I have edited my post. Actually I overlooked the word constant.
1@kaymant sir: in 11, can u please elaborate on how (D) is also correct?
1well in Q 12 there is a local maximum at X=0
66
kaymant
·2010-03-28 15:34:34
The initial momentum of the system (= plank + everything the plank contains) is zero. When the block (B) compresses the left spring maximally, the block must be stationary w.r.t. to the plank (P) and since the velocity of center of mass must remain zero, the speeds of B and P must be zero individually. Energy considerations give the compression of the left spring at this instant as \ell. As such the displacement (in magnitude) of B w.r.t. P is 5\ell
Since displacement of CM is zero, we get that
M\Delta \vec{r}_{PG}+m\Delta \vec{r}_{BG}=0
where \Delta \vec{r}_{PG} denotes the displacement of Plank P w.r.t. the ground G and similarly for the block B. But
\Delta \vec{r}_{BG}=\Delta \vec{r}_{BP}+\Delta\vec{r}_{PG}
Hence we get
\Delta \vec{r}_{PG}=-\dfrac{m}{m+M}\Delta \vec{r}_{BP}
Hence magnitude-wise, we get
|\Delta \vec{r}_{PG}|=\dfrac{m}{m+M}|\Delta \vec{r}_{BP}|=\dfrac{m}{m+M}\,5\ell
Hence (A).
1112)
U(x) cannot have a max in this case....bcoz U(x)=x4(-4/x^2+8)→8x^4 when x→∞....
66
kaymant
·2010-03-28 14:46:49
Edit: (D) is not correct.
Since the rod just reaches the vertical position, its initial angular speed is obtained by
\dfrac{1}{2}\cdot\dfrac{1}{3}m\ell^2 \omega_0^2 = mg\dfrac{\ell}{2} which gives the initial angular speed as
\omega_0=\sqrt{\dfrac{3g}{\ell}}. Hence (B).
This angular speed comes from an impulsive torque which arises due to the magnetic force. If the current I(t) flows through the rod then the torque about the left end is
\tau = \int_0^\ell I(t)Bx\ \mathrm dx= I(t)B\dfrac{\ell^2}{2}
where I have measured the position x from the left end. The impulse of this toque is
\int_0^{\Delta t}\tau \ \mathrm dt = \dfrac{B\ell^2}{2}\int_0^{\Delta t} I(t)\ \mathrm dt= qB\dfrac{\ell^2}{2}
This impulse is responsible for the increment in angular momentum. Hence
qB\dfrac{\ell^2}{2}=\dfrac{1}{3}m\ell^2\omega_0
which gives
q=\dfrac{2m\omega_0}{3B}=\dfrac{2m}{3B}\sqrt{\dfrac{3g}{\ell}}
Hence (A) as well.
66
kaymant
·2010-03-28 14:27:19
(The question number I write below are those which appear before each one in the diagrams)
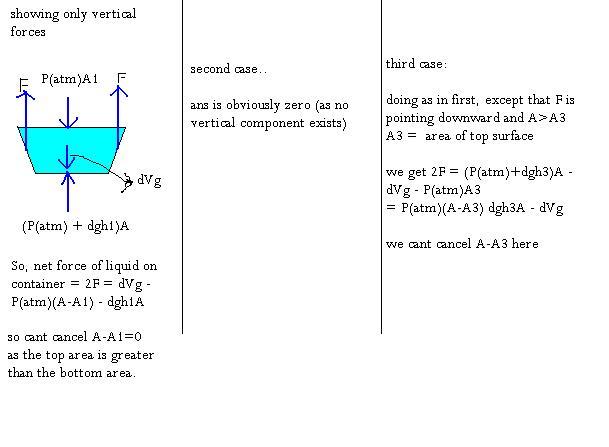
10) Since the pressure at the bottom is p0 + Ïgh.
So (B) is correct trivially.
If you draw the FBD of the fluid alone, then the force of gravity ÏVg pulls it downwards, the reaction from the bottom of the vessels (which is same as p0 + Ïgh) pushes it upwards; the force due to atmosphere is pushes it down; finally the sidewalls exert some force as well the horizontal component of which cancels out while the vertical component survive.
For (i) this vertical component pushes the fluid up; for (ii) the vertical component is absent; while for (iii) this component pushes the fluid down. By balancing out the forces in vertical direction, we get the vertical force (which is also the net force) by the sidewalls as:
for (i) ÏVg &ndash Ïgh1A
for (ii) 0
for (iii) Ïgh3 A &ndash ÏVg
By Newton's third law these are the corresponding forces by the liquid on the sidewalls.
106
Asish Mahapatra
·2010-02-27 23:42:05
@decoder: how can C,D be simultaneously true?
1Q11 i marked A,B,C,D
angluar impulse=> ∫Il2B/2 dt =Iω
ql2B/2=Iω [∫Idt = q]
q=2Iω/l2B
u can easily get ω by energy conservation
1q6
I think this should be correct
I am assuming that left spring also gets displaced by l
so
by conservation of com
let big Plank move x to the right
ml= m(-4l+x) + Mx
ull get x= 5mlm+M
106
Asish Mahapatra
·2010-02-21 22:31:41
make this Q5. to avoid confusion
this is Q6.
