Chain falls, scale gives reading

JEE Mains Help › Mechanics questions › Chain falls, scale gives reading

A chain of mass M and length l is suspended vertically with its
lowest end touching a scale. The chain is released and falls onto the
scale.
What is the reading of the scale when a length of chain, x, has fallen?
(Neglect the size of individual links.)

#Physics #Mechanics

UP 0 DOWN 0 1 4
Post on FacebookPost anonymously?

4 Answers

13

Avik ·2009-12-16 08:24:15

Mgx/2l ...?

UP 0 DOWN 0
Post on FacebookPost anonymously?

1

AD ·2009-12-16 08:35:22

Dunno....don't remember the answer..would you care to elaborate?

UP 0 DOWN 0
Post on FacebookPost anonymously?

1

Anirudh Kumar ·2009-12-17 01:29:37

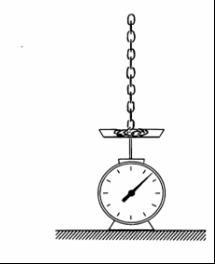
Weight of part of chain already on the scale = Mxg/L .....1

now velocity of the small part ( dm) which falls instantly on the scale = √2gx

thus impulse on the scale = dm √2gx

=> F.dt=dm √2gx (f=impulsive force)
=> F= (M/L)*dx/dt*(√2gx)
=>F= v²M/L
=>f=2gxM/L .............2

thus net force = 3Mgx/L

thus reading = 3MxL

UP 0 DOWN 0
Post on FacebookPost anonymously?

1

AD ·2009-12-17 05:27:05

yeah that's correct.....except of course a typo in the last line

UP 0 DOWN 0
Post on FacebookPost anonymously?

Your Answer

Basic Integral Calculus Operators Symbols Matrix Cases

√ √ || {} [] () → ~ ^ x x x → → ln log lg lim lim cos sin tan cot arcsin arccos arctan

∫ ∫ ∫ ∫ ∫ ∬ ∬ ∬ ∬ ∬ ∭ ∭ ∭ ∭ ∭ ⨌ ⨌ ⨌ ⨌ ⨌

∑ ∑ ∑ ∑ ∑ ∮ ∮ ∮ ∮ ∮ ∏ ∏ ∏ ∏ ∏ ∐ ∐ ∐ ∐ ∐

+ - × ÷ ± ∓ = ∪ ∩ ≠ ∼ ≈ ∅ ∀ ∃ ∈ ∋ ∝ ≤ ≥ ≃ ≅ ≡ < > ≪ ≫ ⊂ ∉ ⊃ ⊆ ⊇ ⇒ ⇐ ⇔ ⇒ ⇐ ⇔ ⇑ ⇓ ⇕ → ← ↔ → ← ↔ ↑ ↓ ↕ ↖ ↗ ↘ ↙ ↪ ↩ ⇀ ↼ ⇁ ↽

° ∂ ∞ α β γ δ θ λ μ ν ξ π ρ σ φ ω ε ƒ κ τ υ Γ Δ Λ Σ Π Ω