A paricle moves in the xy plane accordingly with the velocity v=(a)i+(bt)j. At the instant t=a√3/b the magnitude of the tangential, normal and the toatal acceleration are-___________,
_________ and ________.
I am telling you how to solve this problem.
You have to find the radius of curvature ( i hope you remember the formula ... if not, try to recollect [1] )
After you know R the nomal acceleration will be V2/R
Now Tangential acceleration can be simply calculated by putting value of t in dV/dt expression.
For net acceleration just take the resultant by √at2 + an2
Give it a shot ... you can solve it.
Cheers.
1have been thinking abt this for last 1/2 an hour i think............
how to find the radius of curvature [7] [7]
the curve eqn i got..
tangent we will get through that point at given time.....
but then it will be looooooooooong process.....
lokesh bhaiya mentioned abt some formula ...
any one reply // .... ant any shorter technique//
1haan i googled just now and found this.....
baapre......
anyways ... THANKYOU :)
33:D
thats in NCERT maths book too...
in a question to find its value for a circle... (not specifying what it is ;)
21Priyam : I had read this sumwer is it true ?
Normal Acc = Atotalsinθ
and
Tangential Acc. = Atotalcosθ
IS THIS TRUE??? [7]
33See:
http://wiki.targetiit.com/Mechanics
I wrote tangential and normal acceleration part there.. :P
33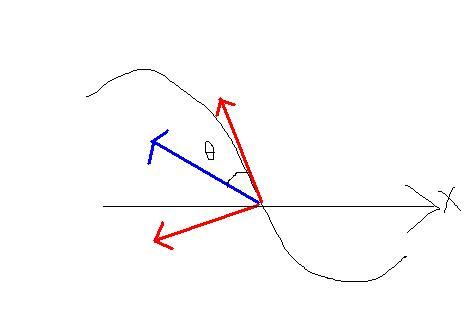
this is the theta not dy/dx (blue is total acc. and red are tang and normal acc...)
