the answer given is (b),(c)
multiple choice...
Q..A car of mass M is moving on a horizontal circular path of radius r.At an instant its speed is v & is increasing at the rate a.............
(a)the acceleration of the car is towrds d centre of the path..
(b)the magnitude of the frictional force on the car is greater than M v2r....
(c)the friction coefficient b/w the ground nd the car is not less than ag......
(d)the friction coefficient b/w the ground nd the car is μ=tan-v2/rg...........
-
UP 0 DOWN 0 0 15

15 Answers
for B part
net acceleration = \sqrt{\frac{v^{2}}{r}+ a }
thus fs > Mv2/r
@Anirudh,
the net acceleration is not \sqrt{\frac{v^2}{r}+a}.
Its actually, \sqrt{\left(\frac{v^2}{r}\right)^2+a^2}
The idea is that the centripetal acceleration and the tangential acceleration both must be provided by the friction. So the net frictional force is
f=m\sqrt{\left(\frac{v^2}{r}\right)^2+a^2}
Since f\le \mu N
so we must have
m\sqrt{\left(\frac{v^2}{r}\right)^2+a^2}\le \mu mg giving
\sqrt{\left(\frac{v^2}{rg}\right)^2+\left(\dfrac{a}{g}\right)^2}\le \mu
eureka radial velocity ?u r talking abt acceleration na ?
by the way i am also having a silly doubt in this ,
i.e in wich direction will dis friction act ??can n e 1 help me wid a figure??
in my notes there is one fig for a similar question where dey hav shown the direction of frictional force in the noninertial frame , but i m getting confused ......
ans to ques b
net frictional force is always greater than mv2/r
this is the frictional force which acts towards the centre due to the tendency of the body to skid out radially
another frictional force acts tangentially in the direction of motion
so net magnitude is> mv2/r
so in wich direction will d car skid if i increase v more than the limiting value ???
jagaran please can u make a figure wich shows the direction of all forces along with direction of skiding please???
@ qwerty i was wrong earlier. the friction in tangential dir does not come into play as its limiting value has alredy been crossed when car is set into motion.
so the frictional force acting towards center is mv2/r =umg where v is the maxm value with which a trn can be made. as lsoon as u cross v friction does not provide force for turning and
car skids tangentially at the pt. where v exceeds maxm speed.
this is final i wont delete the post again
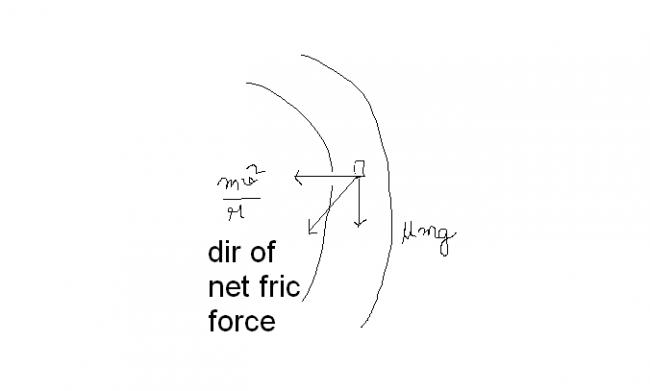
the tangential fric. force is constant and it wont increase on increasing v so it does not affect direction of skidding.
but kaymant sir earlier told that friction itself is providing tangential acceleration [7]
and how is the tangential frictional force = \mumg ???the net frictional force shud be \mumg , if its a limiting case
friction did not produces any accln.it acts against direction of motion.the centripetal accln is also not produced by friction.it acts radially ouwards. friction acts towards centre and is the force which counters the radially outwards accln.
what kayamant sir meant is that friction neutralises the tangential accln.the magnitude remains same either way.