33no i am far far away from the answer [2]
sorry i can't help u here [2]
A uniform disc of mass m and radius r is rolling on a circle by virtue of torque Ï„ given to rod(mass M length L) pivoted to disc.Find angular accelrations of rod and disc.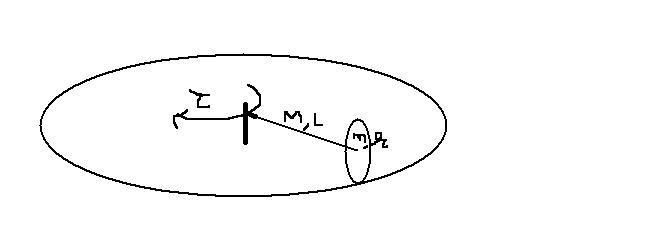
-
UP 0 DOWN 0 0 47
47 Answers
24actually you are very close.....
here are the answers::
Ï„/L2(2M+9m) and Ï„/Lr(2M+9m)
3324Ok..............But can u tell me how u got ang acc of disc= 3Ï„
Lr(M+3m)
33Leave it..
It is wrong...
:(
and u will get confused bekar me..
its not worth solving..
[3](dur ke angur khatte hai isliye)
62There are 2 rotations involved..
in is along the axis of the rod.
the other is by the center..
(Does this hint work enuf for finding the moment of inertia?)
24I have been scratching my head for over a week.............plzzzz send the solution........I am getting mad.......
24I have been scratching my head for over a week.............plzzzz send the solution........I am getting mad.......
1I know the ans is diffcult but iwill find it out Mr. u rekal.
give me some time
62inertia along the axis of the rod is mr2/2
inertia along the center will be ML2/3 + mr2/4+mL2
Just check that this is correct!
1this is correct but how to get the ans. bhaiyya
i wrote some eqns but could not get the ans eureka has given
can you write the eqns. so that i correct mine
62I will try to give some more hints... (I din solve it myslef... but see if this helps!)
Take friction ... call it F
and then find the total torque due to friction and applied torque... at the central rod...
THen use torque = I alpha
again there is torque along the central axis of the rod.. and there is rotation or angular acceleration ... again due to friction alone
also there is a relation between these two torque....
Use the moment of inertias that i put above... i guess that should help :)
1wil the net Ï„ about the central axis be equal to (tau) - FL or will it be something else?
1ok here are my equations please point out the mistake in them
(tau) - FL= Iα (1)
(tau)/L - F = ma where a =αL (2)
Fr =(mr2/2)a/r (3)
but this does not give the ans
[2] what's wrong
maybe 2nd eqn is doubtful
62philip we are dealing with 2 different angular accelerations..
i think in the second equation u have used the same angular acceleration as the first ....