for 2nd one does the velocity of the ball becom parallel to the ground after collision [6]
8 Answers
who said....my mind says that it will undergo the motion like a reflecting ray on spherical mirror....draw tangent which replaces the spherical thing by a flat surface that makes life a lot easier...[1][1][1][1]
thus the vel of ball becomes horizontal only if @=45° which is not given..[3][3][3]
for 1st one is ans this
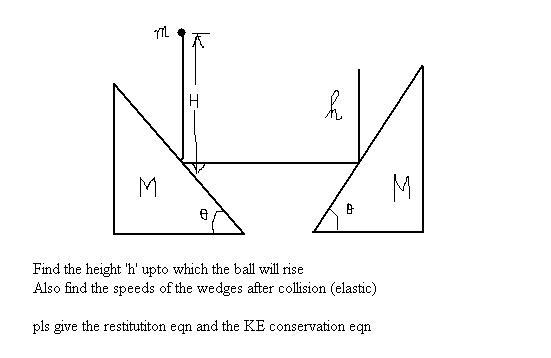
\\ \texttt{velo\: of\: wedges\: }=\frac{m\sqrt{2gH}}{m+M}\\ \texttt{height\: h}=H.\left ( \frac{M-m}{M+m} \right )^{2}
i guess u gave an extra info i.e abt angle
chances of mistake are high as it has been done in a haphazard manner [3]
using usuall cartesian sign convention i.e. upward is positive , downward negative, rightward positive and leftward negative we will proceed in the rest of the problem...[1][1][1]
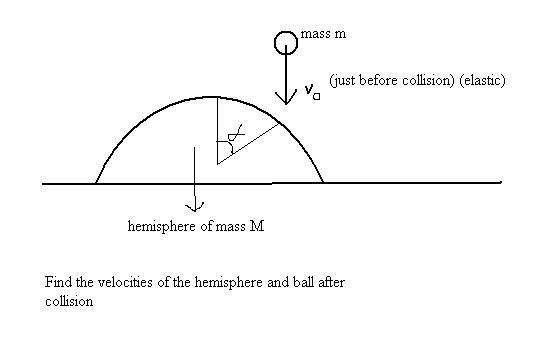
let vel of ball after collision be v1
and that of the spherical mass be v
thus, solving we get |v1|=vosec 2α
and |v|=m/Mvosec 2α
i think the above answer is wrong coz i used momentum conservation while i know that we cannot conserve momentum due to presence of external forces in the system...please suggest a method...[2][2][2][2][2][2][2]
2)
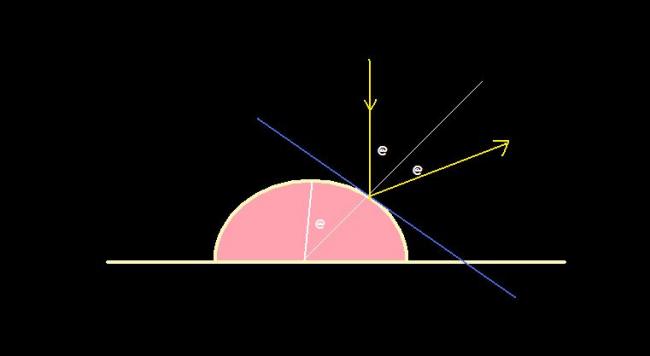
V2 be velo of hemisphere after collision V3 be velo of ball after collison
since collision is elastic we have
1=V2sinα+V3cosαV0cosα...............i
COM in horizontal direction
MV2=mV3cos(90-2α)................................ii
now Conservation OF energy
12mvo2 =12mv32 +12Mv22 ......................iii
@subhomoy.. u can conserve momentum... in the horizontal direction bcz the external impulsive force acts only in the vertical direction (on the system)
but then akari has quite convinced me that the question itself is wrong... ull find that after calculating that the ball cannot be horizontal (unless the impulse on the ball comes out to be zero) which is again contradicting...
So i guess question 1 is cancelled