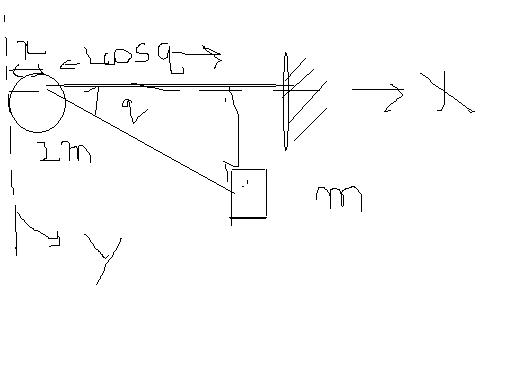
since there is no force in the x direction conserve momentum
2m(0)+m(l)=2m(x )+m(lcosq+x)
solving you get c as answer.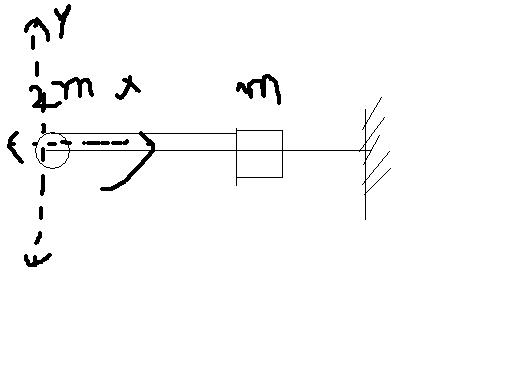
A bead can slide on a smooth straight wire and particle of mass m is attached to the bead by a light string of length L. The particle is held in contact with the wire with the string taut and is then let fall. If the bead has mass 2m. Then When the string makes an angle q with the wire then bead wud hav slipped a distance:
(A) L(1-cos q)
(B) L/2 (1-cos q)
(C) L/3 (1-cos q)
(D) L/6 (1-cos q)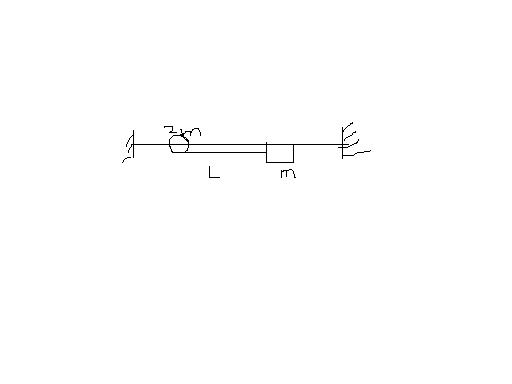
since there is no force in the x direction conserve momentum
2m(0)+m(l)=2m(x )+m(lcosq+x)
solving you get c as answer.

Simply used the fact that COM of the bead-block system remains stationary in the horizontal direction
2mx = m {L(1 - cosq) - x }
or x = L3(1 - cosq) u sud hav given that the angle is made with horizontal
i hav the shortest method : COM is at a distance of L/3 frm 2m
at q = 90o 2m will hav moved by L/3 . put q= 90 in the options , C is the answer [3] [3]