1i think for the 1st time the answer to such a tough sum was thought out be me !!!!!!!!! D:
anyways as usual gr8 solution by kaymant
A weightless rod of length l with a small load of mass m at the end is hinged ar point A and occupies a strictly vertical position, touching a body of mass M.A slight jerk sets the system in motion. Frixtion is neglected and l=0.2m....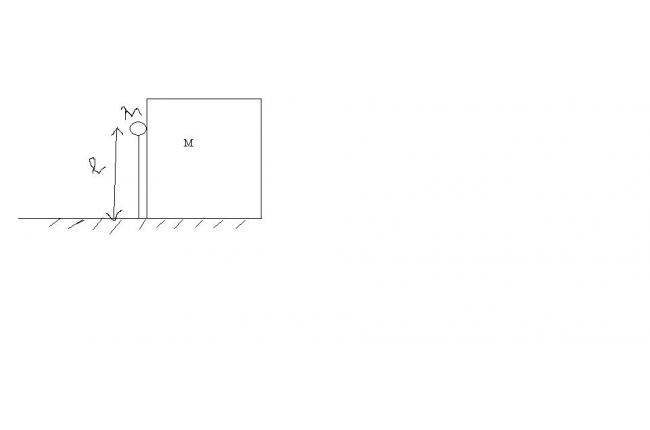
1. At any instant efore seperation, the angle made by the rod with horizontal is θ . If accl. of M is a and its velocity is v, then tangential accl. oof the small mass m is -----------------
2.The ratio M/mfor the two bodies m and m to seperate at the the instant θ=π/6 is---------------------------
3.Velocity of the mass m at the moment of seperation is -----------------
-
UP 0 DOWN 0 1 22
22 Answers
1
66The velocity of m at the instant when it leave contact with the block = √gl/2
66Continuation of my previous post....
The FBD of the bob m: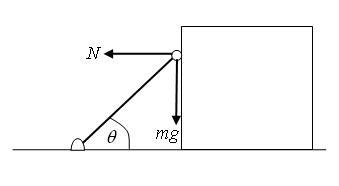
Since m is moving in a circle, the centripetal acceleration is supplied by components of N and mg. So we get
N\cos\theta+mg\sin\theta = m\omega^2\ell
When it leaves contact with the block, N = 0 and θ = π/6. First, at θ = π/6, we get
\omega^2 = \dfrac{g}{\ell}\cdot \dfrac{1}{1+\frac{M}{4m}}
Hence, we have by setting N = 0, we get
\dfrac{g}{2} = g \dfrac{1}{1+\frac{M}{4m}}
i.e.
\boxed{\dfrac{M}{m}=4}
66When the rod makes an angle θ with the horizontal, let the velocity of the block M be V while its acceleration be aM. At this instant, let the angular velocity of the rod about the hinge A be ω.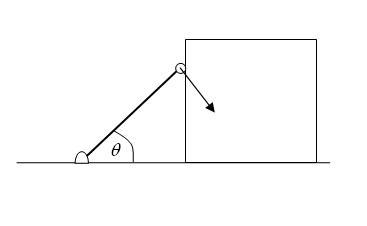
Since the bob is in contact with the block, the horizontal velocity of the bob must be V. Therefore
\omega \ell\sin\theta =V
Next, energy conservation gives
mg\ell(1-\sin\theta)=\dfrac{1}{2}MV^2+\dfrac{1}{2}m\ell^2\omega^2
Eliminating V gives
mg\ell(1-\sin\theta)=\dfrac{1}{2}M\omega^2\ell^2\sin^2\theta+\dfrac{1}{2}m\ell^2\omega^2=\dfrac{1}{2}\omega^2\ell^2(m+M\sin^2\theta)
which gives
\omega^2=\dfrac{2mg(1-\sin\theta)}{\ell(m+M\sin^2\theta)}
Differentiate w.r.t. t and use the fact that \omega=-\dfrac{\mathrm d\theta}{\mathrm dt}, we get the angular acceleration \dfrac{\mathrm d\omega}{\mathrm dt}=\dfrac{g}{\ell}\cdot\dfrac{m\cos\theta(m+M\sin\theta(2-\sin\theta))}{(m+M\sin^2\theta)^2}
Hence the tangential acceleration of the bob is
a_t=g\cdot\dfrac{m\cos\theta(m+M\sin\theta(2-\sin\theta))}{(m+M\sin^2\theta)^2}
Also, the acceleration aM of the block is
a_M=\dfrac{\mathrm dV}{\mathrm dt}=\ell\left(\sin\theta \dfrac{\mathrm d\omega}{\mathrm dt}+\omega \cos\theta\dfrac{\mathrm d\theta}{\mathrm dt}\right)=\ell\left(\sin\theta \dfrac{\mathrm d\omega}{\mathrm dt}-\omega^2 \cos\theta\right)
Solving for the tangential acceleration at in terms of aM and V we get
\boxed{a_t = \dfrac{a_M\sin\theta + (V^2/\ell)\cos\theta}{\sin^2\theta}}
as the answer to the first part.
1shortcut for relation between vel
vel of m is wl
w=d@/dt i think this should be enugh!
1lets luk like unfortunately i solved the sum withouth seeing nishants sirs hint
first let the angle with the horizontal be @
thereofre we can find the relation ship between vel of M an m simple
so after finding out
mgh=1/2Mv^2+1/2mv^2
now dv/dt is tangential acc yeah!!!!!!
3correct ans kya hai ???
sriraghav can u plzz post the ans also ?? not the soln, but the just the final ans ...
62Hint:
1) Write the constraint equation for any general theta
2) At any theta, write Energy, differentiate it wrt time equate to zero (conservation of energy)! This will give acceleration.
1arrey at that point acceleration diya hai......
so N = Ma
rest watever is there can go to hell.......
11N wouldnt be a constant
it would depend on the vel i think but yet not solved fully
11i have another doubt with the question
(and this answers ur doubt i think philip)
the small mass goes to the left or right when it is jerked????
1hinge hai toh bottommost point hoga figure mein
first anyone answer my doubt ????[7][7]
1can someone explain why or how velocity of mass M is needed for first part... [7][7]
on ly forces that'll contribute to tangential acceleration will be mg and N na???
someone plz see this